
已知函数
(1)若x=2为 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若 在
在 上为增函数,求实数a的取值范围.
上为增函数,求实数a的取值范围.
(1)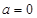 ;(2)
;(2) 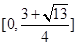
解析试题分析:(1)通过求导可得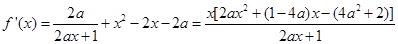 .又因为x=2是极值点.即可求得
.又因为x=2是极值点.即可求得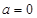 .
.
(2)通过对对数的定义域可得符合题意的不等式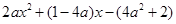
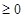 .在
.在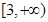 上恒成立.所以转化为研究二次函数的最值问题.通过对称轴研究函数的单调性即可得到结论.本题的的关键是对含参的函数的最值的讨论.以二次的形式为背景紧扣对称轴这个知识点.
上恒成立.所以转化为研究二次函数的最值问题.通过对称轴研究函数的单调性即可得到结论.本题的的关键是对含参的函数的最值的讨论.以二次的形式为背景紧扣对称轴这个知识点.
试题解析:(1)因为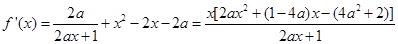 .因为x=2为f(x)的极值点.所以
.因为x=2为f(x)的极值点.所以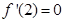 即
即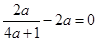 .解得
.解得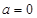 .又当
.又当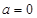 时
时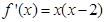 .从而x=2为f(x)的极值点成立.
.从而x=2为f(x)的极值点成立.
(2)因为f(x)在区间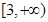 上为增函数.所以
上为增函数.所以 .在区间
.在区间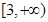 上恒成立. ①当
上恒成立. ①当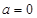 时.
时. 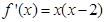
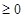 在
在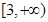 上恒成立.所以f(x)在
上恒成立.所以f(x)在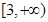 上为增函数.故
上为增函数.故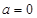 符合题意.②当
符合题意.②当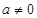 时.由函数f(x)的定义域可知,必须有
时.由函数f(x)的定义域可知,必须有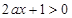 时
时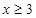 恒成立.故只能
恒成立.故只能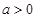 .所以
.所以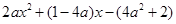
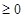 在区间
在区间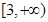 上恒成立.令g(x)=
上恒成立.令g(x)= 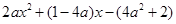 .其对称轴为
.其对称轴为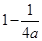 .因为
.因为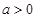 .所以
.所以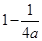 <1.从而g(x)
<1.从而g(x) 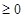 在
在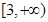 上恒成立.只需要g(3)
上恒成立.只需要g(3) 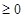 即可.由g(3)=
即可.由g(3)= 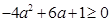 .解得:
.解得: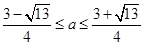 .因为
.因为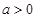 .所以
.所以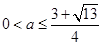 .综上所述.
.综上所述.  的取值范围为
的取值范围为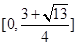 .
.
考点:1.对数函数的知识点.2.最值问题.3.含参的讨论.


科目:高中数学 来源: 题型:解答题
已知函数 的定义域为
的定义域为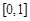 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的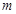 (
(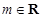 且
且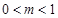 ),存在
),存在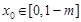 ,使得
,使得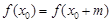 ,则称
,则称 具有性质
具有性质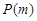 .
.
(1)已知函数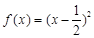 ,
,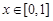 ,判断
,判断 是否具有性质
是否具有性质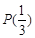 ,并说明理由;
,并说明理由;
(2)已知函数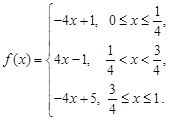 若
若 具有性质
具有性质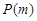 ,求
,求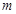 的最大值;
的最大值;
(3)若函数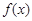 的定义域为
的定义域为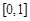 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足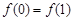 ,
,
求证:对任意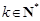 且
且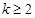 ,函数
,函数 具有性质
具有性质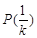 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“地沟油”严重危害了人民群众的身体健康,某企业在政府部门的支持下,进行技术攻关,新上了一种从“食品残渣”中提炼出生物柴油的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似的表示为: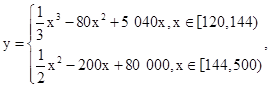
且每处理一吨“食品残渣”,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将补贴.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式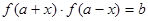 对定义域中的每一个
对定义域中的每一个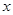 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数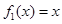 是否为“(
是否为“( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数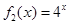 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对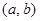 ;
;
(3)已知函数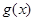 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对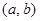 为(1,4).当
为(1,4).当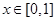 时,
时,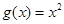
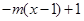
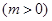 ,若当
,若当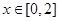 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 的导函数的图像与直线
的导函数的图像与直线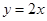 平行,且
平行,且 在
在 处取得极小值
处取得极小值 .设
.设 .
.
(1)若曲线 上的点
上的点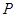 到点
到点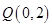 的距离的最小值为
的距离的最小值为 ,求
,求 的值;
的值;
(2)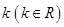 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对定义在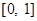 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为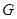 函数。
函数。
①对任意的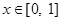 ,总有
,总有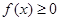 ;
;
②当 时,总有
时,总有 成立。
成立。
已知函数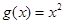 与
与 是定义在
是定义在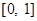 上的函数。
上的函数。
(1)试问函数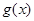 是否为
是否为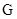 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是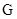 函数,求实数
函数,求实数 的值;
的值;
(3)在(2)的条件下,讨论方程
 解的个数情况。
解的个数情况。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com