
对定义在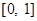 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为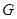 函数。
函数。
①对任意的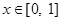 ,总有
,总有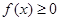 ;
;
②当 时,总有
时,总有 成立。
成立。
已知函数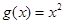 与
与 是定义在
是定义在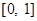 上的函数。
上的函数。
(1)试问函数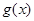 是否为
是否为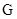 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是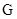 函数,求实数
函数,求实数 的值;
的值;
(3)在(2)的条件下,讨论方程
 解的个数情况。
解的个数情况。
(1)函数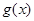 是
是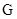 函数,(2)
函数,(2) 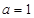 (3)
(3)
解析试题分析:
(1)根据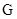 函数的定义,验证
函数的定义,验证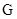 函数的两个条件,即可判断;
函数的两个条件,即可判断;
(2)根据因为函数 是
是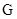 函数,利用
函数,利用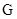 函数的两个条件,即可求得实数
函数的两个条件,即可求得实数 的值;
的值;
(3)根据(2)知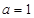 ,原方程可以化为
,原方程可以化为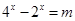 ,再利用换元法,即可求实数
,再利用换元法,即可求实数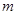 的取值范围.
的取值范围.
对考查新定义的题要与熟悉的已知函数性质比较,参考其性质及运算特征进行计算,对新定义熟悉性质后求参数的取值,把方程解的情况转化成求值域,利用换元法、配方法求函数的值域;解题的关键是正确理解新定义.
试题解析:
(1)当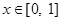 时,总有
时,总有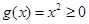 满足①
满足①
当 时
时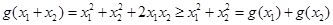 满足②
满足②
所以函数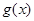 是
是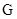 函数.
函数.
(2)
Ⅰ当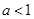 时,
时,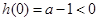 不满足①,所以不是是
不满足①,所以不是是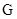 函数
函数
Ⅱ当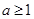 时,
时,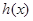 在
在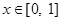 上是增函数,则
上是增函数,则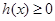 ,满足①
,满足①
由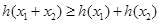 ,得
,得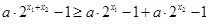
即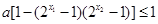
因为
所以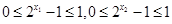 ,
,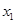 与
与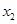 不同时等于1
不同时等于1
所以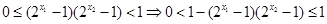
所以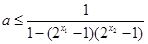
当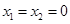 时,
时, 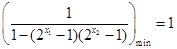 即
即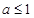 于是
于是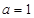
综上所述: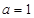
(3) 根据(2)知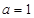 ,原方程可以化为
,原方程可以化为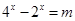
由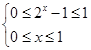 得
得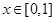
令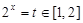 ,则
,则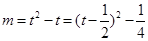 在
在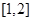 单调递增且值域为
单调递增且值域为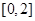
所以,当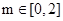 时,方程有一解
时,方程有一解
当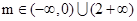 时方程无解
时方程无解
考点:函数恒成立问题.


科目:高中数学 来源: 题型:解答题
我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数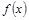 与第x天近似地满足
与第x天近似地满足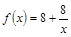 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费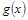 近似地满足
近似地满足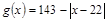 (元).
(元).
(1)求该村的第x天的旅游收入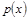 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,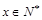 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数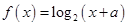 .
.
(1)若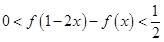 ,当
,当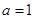 时,求
时,求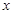 的取值范围;
的取值范围;
(2)若定义在 上奇函数
上奇函数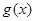 满足
满足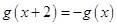 ,且当
,且当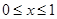 时,
时,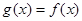 ,求
,求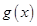 在
在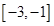 上的反函数
上的反函数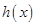 ;
;
(3)对于(2)中的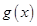 ,若关于
,若关于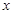 的不等式
的不等式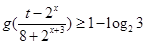 在
在 上恒成立,求实数
上恒成立,求实数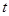 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一条笔直的工艺流水线上有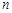 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图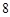 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为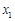 ,
,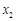 ,
,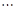 ,
,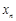 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.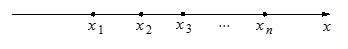
(Ⅰ)若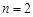 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)若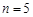 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为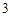 ,
,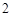 ,
,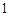 ,
,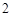 ,
,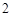 ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知偶函数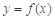 满足:当
满足:当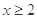 时,
时,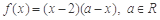 ,当
,当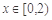 时,
时,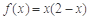 .
.
(1)求当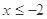 时,
时,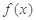 的表达式;
的表达式;
(2)试讨论:当实数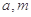 满足什么条件时,函数
满足什么条件时,函数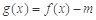 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一种放射性元素,最初的质量为 ,按每年
,按每年 衰减.
衰减.
(1)求 年后,这种放射性元素的质量
年后,这种放射性元素的质量 与
与 的函数关系式;
的函数关系式;
(2)求这种放射性元素的半衰期(质量变为原来的 时所经历的时间).(
时所经历的时间).( )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com