
已知偶函数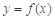 满足:当
满足:当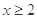 时,
时,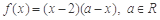 ,当
,当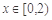 时,
时,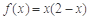 .
.
(1)求当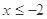 时,
时,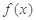 的表达式;
的表达式;
(2)试讨论:当实数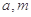 满足什么条件时,函数
满足什么条件时,函数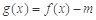 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.
(1)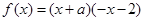 ;(2)①
;(2)①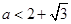 时,
时,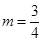 ;②
;②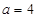 时,
时,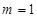 ;③
;③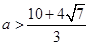 时,
时,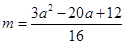 .
.
解析试题分析:本题考查函数的奇偶性、函数解析式、函数零点问题以及等差数列的定义,考查化归与转化思想,考查计算能力.第一问,先把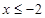 转化成
转化成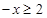 ,利用已知
,利用已知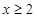 时的解析式,利用偶函数转化解析式;第二问,把
时的解析式,利用偶函数转化解析式;第二问,把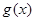 有4个零点,先转化为
有4个零点,先转化为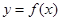 与
与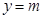 有4个交点且均匀分布,所以利用等差中项,偶函数等基础知识列出表达式,分情况进行讨论分析.
有4个交点且均匀分布,所以利用等差中项,偶函数等基础知识列出表达式,分情况进行讨论分析.
试题解析:(1)设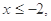 则
则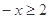 ,
,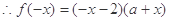 ,
,
又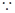
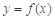 偶函数
偶函数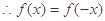 ,
,
所以,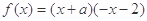 .
.
(2)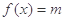 零点
零点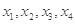 ,
,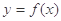 与
与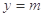 交点有4个且均匀分布,
交点有4个且均匀分布,
(Ⅰ)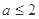 时,
时, 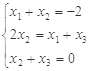 得
得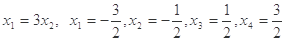 ,
,
所以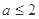 时,
时,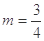 ,
,
(Ⅱ)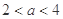 且
且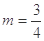 时 ,
时 ,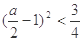 ,
, 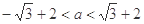 ,
,
所以 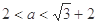 时,
时,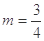 ,
,
(Ⅲ)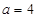 时
时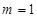 时,符合题意,
时,符合题意,
(Ⅳ)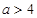 时,
时,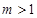 ,
,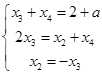 ,
,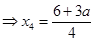 ,
,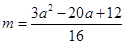 ,
,
此时,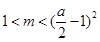 ,所以
,所以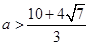 或
或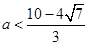 (舍)
(舍)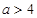 且
且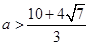 时,
时,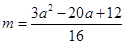 时存在.
时存在.
综上,①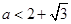 时,
时,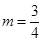 ;
;
②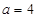 时,
时,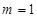 ;
;
③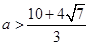 时,
时,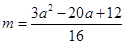 符合题意.
符合题意.
考点:1.求函数解析式;2.函数零点问题;3.图像交点问题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式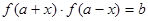 对定义域中的每一个
对定义域中的每一个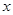 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数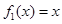 是否为“(
是否为“( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数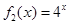 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对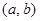 ;
;
(3)已知函数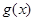 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对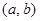 为(1,4).当
为(1,4).当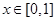 时,
时,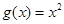
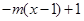
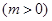 ,若当
,若当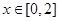 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 的导函数的图像与直线
的导函数的图像与直线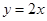 平行,且
平行,且 在
在 处取得极小值
处取得极小值 .设
.设 .
.
(1)若曲线 上的点
上的点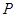 到点
到点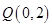 的距离的最小值为
的距离的最小值为 ,求
,求 的值;
的值;
(2)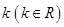 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对定义在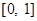 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为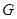 函数。
函数。
①对任意的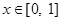 ,总有
,总有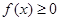 ;
;
②当 时,总有
时,总有 成立。
成立。
已知函数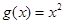 与
与 是定义在
是定义在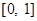 上的函数。
上的函数。
(1)试问函数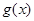 是否为
是否为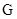 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是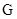 函数,求实数
函数,求实数 的值;
的值;
(3)在(2)的条件下,讨论方程
 解的个数情况。
解的个数情况。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
运货卡车以每小时 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米
 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用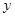 关于
关于 的表达式;
的表达式;
(2)当 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com