
已知函数 (
(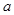 是常数且
是常数且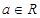 )
)
(1)若函数 的一个零点是1,求
的一个零点是1,求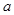 的值;
的值;
(2)求 在
在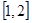 上的最小值
上的最小值 ;
;
(3)记 若
若 ,求实数
,求实数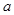 的取值范围。
的取值范围。
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析试题分析:(1)因为1是 的一个零点,将1代入得
的一个零点,将1代入得 ,求得
,求得 ;(2)由题意
;(2)由题意 ,先讨论二次项系数
,先讨论二次项系数 ,得最小值
,得最小值 ,然后讨论对称轴
,然后讨论对称轴 分别位于区间
分别位于区间 的各种情况,求出
的各种情况,求出 的最小值,合并得到
的最小值,合并得到 的最小值
的最小值 ,注意分类讨论时不重不漏;(3)由题意
,注意分类讨论时不重不漏;(3)由题意 即相当于
即相当于 恒成立,分离参数即可得
恒成立,分离参数即可得 恒成立,令
恒成立,令 ,
, ,分
,分 求得
求得 的最大值为
的最大值为 ,所以
,所以 .
.
试题解析:(1)由题意知 2分
2分
(2)
 ⅰ当
ⅰ当 时
时 3分
3分
ⅱ当 时,对称轴为
时,对称轴为
 4分
4分
ⅲ当 时,抛物线开口向下,对称轴
时,抛物线开口向下,对称轴
若 即
即 时,
时,
若 即
即 时,
时,
若 即
即 时,
时, 7分
7分
综上所述, 8分
8分
(3)由题意知:不等式 无解
无解
即 恒成立 10分
恒成立 10分
即 对任意
对任意 恒成立 11分
恒成立 11分
令 则
则 对任意
对任意 恒成立12分
恒成立12分
ⅰ当 时
时 13分
13分
ⅱ当 时
时 14分
14分
ⅲ当 时
时
 15分
15分 即
即 16分
16分
考点:1、函数的零点;2、二次函数在给定区间上的最值;3、分离参数处理恒成立问题;4、分类讨论思想.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
方便、快捷、实惠的电动车是很多人的出行工具。可是,随着电动车的普及,它的安全性也越来越受到人们关注。为了出行更安全,交通部门限制电动车的行驶速度为24km/h。若某款电动车正常行驶遇到紧急情况时,紧急刹车时行驶的路程S(单位:m)和时间t(单位:s)的关系为: 。
。
(Ⅰ)求从开始紧急刹车至电动车完全停止所经过的时间;
(Ⅱ)求该款车正常行驶的速度是否在限行范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知偶函数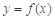 满足:当
满足:当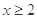 时,
时,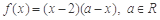 ,当
,当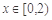 时,
时,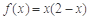 .
.
(1)求当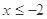 时,
时,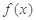 的表达式;
的表达式;
(2)试讨论:当实数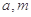 满足什么条件时,函数
满足什么条件时,函数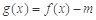 有4个零点,且这4个零点从小到大依次构成等差数列.
有4个零点,且这4个零点从小到大依次构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一种放射性元素,最初的质量为 ,按每年
,按每年 衰减.
衰减.
(1)求 年后,这种放射性元素的质量
年后,这种放射性元素的质量 与
与 的函数关系式;
的函数关系式;
(2)求这种放射性元素的半衰期(质量变为原来的 时所经历的时间).(
时所经历的时间).( )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在不考虑空气阻力的情况下,火箭的最大速度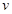 (单位:
(单位: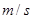 )和燃料的质量
)和燃料的质量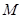 (单位:
(单位: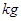 ),火箭(除燃料外)的质量
),火箭(除燃料外)的质量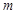 (单位:
(单位: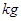 )满足
)满足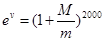 .(
.(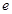 为自然对数的底)
为自然对数的底)
(Ⅰ)当燃料质量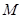 为火箭(除燃料外)质量
为火箭(除燃料外)质量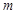 两倍时,求火箭的最大速度(单位:
两倍时,求火箭的最大速度(单位: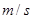 );
);
(Ⅱ)当燃料质量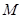 为火箭(除燃料外)质量
为火箭(除燃料外)质量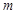 多少倍时,火箭的最大速度可以达到8
多少倍时,火箭的最大速度可以达到8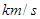 .(结果精确到个位,数据:
.(结果精确到个位,数据: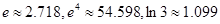 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com