
某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18-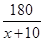 ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2=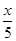 (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;
(2)在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
(1) 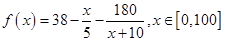 ;(2) 分别用20万元和80万元资金投资A、B两种金融产品,可以使公司获得最大利润,最大利润为28万元.
;(2) 分别用20万元和80万元资金投资A、B两种金融产品,可以使公司获得最大利润,最大利润为28万元.
解析试题分析:(1)根据题意,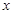 万元资金投入
万元资金投入 产品,利润
产品,利润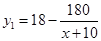 万元;
万元;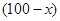 万元资金投入
万元资金投入 产品,利润
产品,利润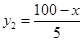 ,由
,由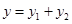 可得所求函数关系;
可得所求函数关系;
(2)由(1)所得函数的解析式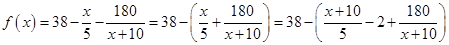
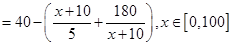 可考虑用基本不等式法求其最大值,并注意等号成立的条件。
可考虑用基本不等式法求其最大值,并注意等号成立的条件。
试题解析:(1)其中x万元资金投入A产品,则剩余的100-x(万元)资金投入B产品,利润总和
f(x)=18-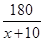 +
+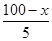
=38-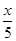 -
-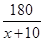 (x∈[0,100]). 6分
(x∈[0,100]). 6分
(2)∵f(x)=40-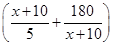 ,x∈[0,100],
,x∈[0,100],
∴由基本不等式得:
f(x)≤40-2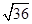 =28,取等号当且仅当
=28,取等号当且仅当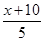 =
=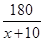 时,即x=20. 12分
时,即x=20. 12分
答:分别用20万元和80万元资金投资A、B两种金融产品,可以使公司获得最大利润,最大利润为28万元. 13分
考点:1、函数在解决实际问题中的应用;2、基本不等式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
对定义域分别是Df,Dg的函数y=f(x),y=g(x),规定:函数h(x)=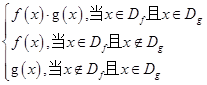
(1)若函数f(x)=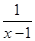 ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式;
(2)求问题(1)中函数h(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x).当年产量不足80千件时,C(x)= x2+10x(万元);当年产量不小于80千件时,C(x)=51x+
x2+10x(万元);当年产量不小于80千件时,C(x)=51x+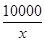 -1 450(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
-1 450(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)2万件.
(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润L最大?并求出L的最大值Q(a).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数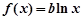 ,
,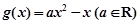
(1)若曲线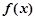 与
与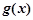 在公共点
在公共点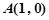 处有相同的切线,求实数
处有相同的切线,求实数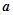 、
、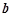 的值;
的值;
(2)当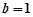 时,若曲线
时,若曲线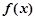 与
与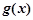 在公共点
在公共点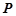 处有相同的切线,求证:点
处有相同的切线,求证:点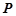 唯一;
唯一;
(3)若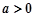 ,
,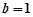 ,且曲线
,且曲线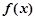 与
与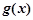 总存在公切线,求正实数
总存在公切线,求正实数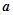 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的定义域为
的定义域为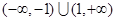 ,对定义域内的任意x,满足
,对定义域内的任意x,满足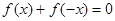 ,当
,当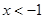 时,
时,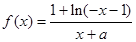 (a为常),且
(a为常),且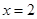 是函数
是函数 的一个极值点,
的一个极值点,
(1)求实数a的值;
(2)如果当 时,不等式
时,不等式 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(3)求证: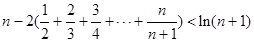
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的定义域为
的定义域为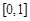 ,且
,且 的图象连续不间断. 若函数
的图象连续不间断. 若函数 满足:对于给定的
满足:对于给定的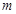 (
(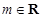 且
且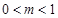 ),存在
),存在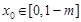 ,使得
,使得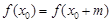 ,则称
,则称 具有性质
具有性质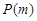 .
.
(1)已知函数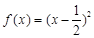 ,
,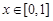 ,判断
,判断 是否具有性质
是否具有性质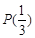 ,并说明理由;
,并说明理由;
(2)已知函数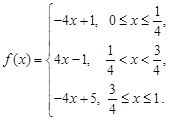 若
若 具有性质
具有性质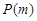 ,求
,求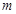 的最大值;
的最大值;
(3)若函数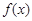 的定义域为
的定义域为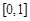 ,且
,且 的图象连续不间断,又满足
的图象连续不间断,又满足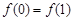 ,
,
求证:对任意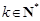 且
且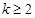 ,函数
,函数 具有性质
具有性质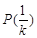 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式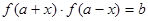 对定义域中的每一个
对定义域中的每一个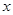 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数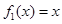 是否为“(
是否为“( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数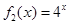 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对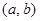 ;
;
(3)已知函数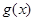 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对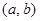 为(1,4).当
为(1,4).当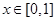 时,
时,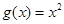
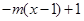
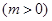 ,若当
,若当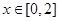 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com