
 中,
中,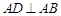 ,
,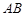 ∥
∥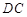 ,
,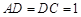 ,
,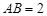 ,动点
,动点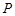 在以点
在以点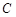 为圆心,且与直线
为圆心,且与直线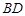 相切的圆上或圆内移动,设
相切的圆上或圆内移动,设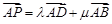 (
(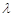 ,
,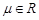 ),则
),则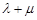 取值范围是
取值范围是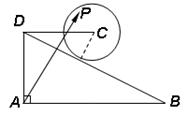
A.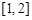 | B.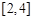 | C.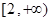 | D.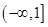 |
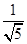 =R
=R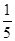
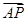 =(x+1,y+1)=
=(x+1,y+1)=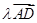 +
+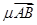 =(
=(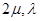 )
)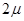 ="x+1,"
="x+1," 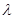 =y+1 ∴ (
=y+1 ∴ (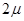 -1)²+(
-1)²+(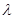 -1)²≤
-1)²≤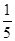
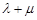 达到最大值, 此时:(
达到最大值, 此时:(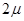 -1)²+(
-1)²+(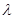 -1)²=
-1)²=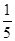
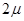 -1=
-1=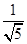 cosA,
cosA,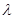 -1=
-1=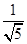 sinA 所以
sinA 所以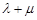 =
=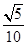 (cosA+2sinA)+
(cosA+2sinA)+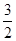
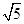 sin(A+B) 所以最大值取
sin(A+B) 所以最大值取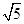 ,所以
,所以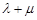 的最大值为
的最大值为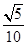 X
X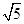 +
+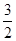 =2
=2

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com