
分析 ①根据指数函数和对数函数的性质进行判断.
②根据对数函数的性质进行判断.
③根据特称命题的否定是全称命题进行判断.
④根据否命题的定义进行判断.
解答 解:①当x∈(0,1),($\frac{1}{2}$)x>0,log${\;}_{\frac{1}{2}}}$x<0.
∴?x∈(0,1),($\frac{1}{2}$)x>log${\;}_{\frac{1}{2}}}$x.故①正确,
②当k=0时,满足k∈[0,8),但此时y=log2(kx2+kx+2)=log22=1,此时函数的值域为{1},不是R.故②错误
③“存在x∈R,(${\frac{1}{2}}$)x+2x≤5”的否定是”任意x∈R,(${\frac{1}{2}}$)x+2x>5”,故③错误,
④“若x∈(1,5),则f(x)=x+$\frac{1}{x}$≥2”的否命题是“若x∈(-∞,1]∪[5,+∞),则f(x)=x+$\frac{1}{x}$<2”,正确,故④正确,
故答案为:①④.
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 0 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{6}$ | B. | x=$\frac{11π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
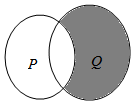 已知集合P={x|y=$\frac{1}{\sqrt{4-x}}$},Q={y|y=log2(x2+4)},集合P与集合Q所对应的韦恩图如图所示,则图中阴影部分表示的集合是( )
已知集合P={x|y=$\frac{1}{\sqrt{4-x}}$},Q={y|y=log2(x2+4)},集合P与集合Q所对应的韦恩图如图所示,则图中阴影部分表示的集合是( )| A. | {x|2≤x<4} | B. | {x|x<2} | C. | {x|x≥4} | D. | {x|x<2,或x≥4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com