
| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理y(分) | 87 | 89 | 89 | 92 | 93 |
分析 由题意,计算$\overline{x}$、$\overline{y}$,求出对应的回归系数$\widehat{b}$、$\widehat{a}$,写出回归方程即可.
解答 解:由题意,计算$\overline{x}$=$\frac{1}{5}$×(89+91+93+95+97)=93,
$\overline{y}$=$\frac{1}{5}$×(87+89+89+92+93)=90,
∴$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{(89-93)×(87-90)+…+(97-93)×(93-90)}{{(89-93)}^{2}+…{+(97-93)}^{2}}$≈0.75,
又线性回归方程过样本中心点,
∴$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=90-0.75×93=20.25,
∴y关于x的线性回归方程为$\stackrel{∧}{y}$=0.75x+20.25.
点评 本题考查了线性回归方程的求法与应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
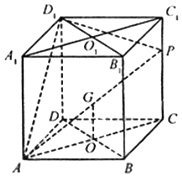 如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m
如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1) | B. | (1,2] | C. | [-2,-1) | D. | (-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,
如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x3•x2=x5 | B. | x+x2=x3 | C. | 2x3÷x2=x | D. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 16 | 22 | 77 | 94 | 39 | 49 | 54 | 43 | 54 | 82 | 17 | 37 | 93 | 23 | 78 | 87 | 35 | 20 | 96 | 43 |
| 84 | 42 | 17 | 53 | 31 | 57 | 24 | 55 | 06 | 88 | 77 | 04 | 74 | 47 | 67 | 21 | 76 | 33 | 50 | 25 |
| A. | 23 | B. | 37 | C. | 35 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{1}{8}$] | B. | [-1,0]∪(0,$\frac{1}{8}$] | C. | [-1,0] | D. | [-1,$\frac{1}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n<m | B. | n>m | C. | n=m | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com