
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,动点
,动点![]() 在线段
在线段![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,则下列结论中正确的是______________.
的中点,则下列结论中正确的是______________.
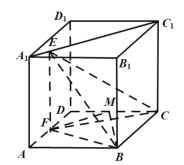
①![]() 与
与![]() 所成角为
所成角为![]() ;
;
②![]() 平面
平面![]() ;
;
③存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
④三棱锥![]() 的体积为定值.
的体积为定值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】2018年,南昌市召开了全球VR产业大会,为了增强对青少年VR知识的普及,某中学举行了一次普及VR知识讲座,并从参加讲座的男生中随机抽取了50人,女生中随机抽取了70人参加VR知识测试,成绩分成优秀和非优秀两类,统计两类成绩人数得到如下的列联表:
优秀 | 非优秀 | 总计 | |
男生 | a | 35 | 50 |
女生 | 30 | d | 70 |
总计 | 45 | 75 | 120 |
(1)确定a,d的值;
(2)试判断能否有90%的把握认为VR知识的测试成绩优秀与否与性别有关;
(3)为了宣传普及VR知识,从该校测试成绩获得优秀的同学中按性别采用分层抽样的方法,随机选出6名组成宣传普及小组.现从这6人中随机抽取2名到校外宣传,求“到校外宣传的2名同学中至少有1名是男生”的概率.
附:![]()
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,
,![]() 是椭圆上的一点,且
是椭圆上的一点,且![]() 在第一象限内,过
在第一象限内,过![]() 且斜率等于-1的直线与椭圆
且斜率等于-1的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
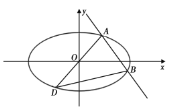
(1)证明:直线![]() 的斜率为定值;
的斜率为定值;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为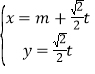 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,椭圆
轴正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() ,其左焦点
,其左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求椭圆![]() 的内接矩形面积的最大值.
的内接矩形面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,E是AD的中点,O是AC与BE的交点.将
,E是AD的中点,O是AC与BE的交点.将![]() 沿BE折起到图2中
沿BE折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.
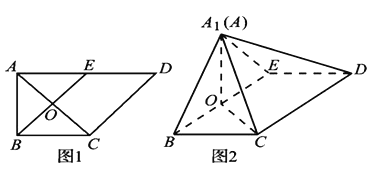
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 与平面
与平面![]() 夹角(锐角)的余弦值.
夹角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有若干扑克牌:6张牌面分别是2,3,4,5,6,7的扑克牌各一张,先后从中取出两张.若每次取后放回,连续取两次,点数之和是偶数的概率为![]() ;若每次取后不放回,连续取两次,点数之和是偶数的概率为
;若每次取后不放回,连续取两次,点数之和是偶数的概率为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.以上三种情况都有可能
D.以上三种情况都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com