练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】现有若干扑克牌：6张牌面分别是2，3，4，5，6，7的扑克牌各一张，先后从中取出两张.若每次取后放回，连续取两次，点数之和是偶数的概率为；若每次取后不放回，连续取两次，点数之和是偶数的概率为，则（ ）

    A.B.C.D.以上三种情况都有可能

    【答案】A

    【解析】

    根据概率公式求出和，即可求得答案.

    6张牌面分别是2，3，4，5，6，7的扑克牌各一张，先后从中取出两张，若每次取后放回

    实验的情况的总数为：

    当先后从中取出两张.若每次取后放回，连续取两次，点数之和是偶数

    情况的总数为：

    ，

    6张牌面分别是2，3，4，5，6，7的扑克牌各一张，先后从中取出两张，若每次取后不放回

    实验的情况的总数为：

    当先后从中取出两张. 若每次取后不放回，连续取两次，点数之和是偶数

    情况的总数为：

    ，

    .

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中， ， ，点分别为的中点.

    （1）证明： 平面；

    （2）若，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方体的棱长为，动点在线段上，、分别是、的中点，则下列结论中正确的是______________.

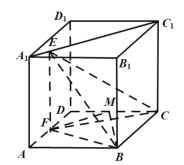
    ①与所成角为；

    ②平面；

    ③存在点，使得平面平面；

    ④三棱锥的体积为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】教育部日前出台《关于普通高中学业水平考试的实施意见》，根据意见，学业水平考试成绩以“等级”或“合格、不合格”呈现.计入高校招生录取总成绩的学业水平考试的3个科目成绩以等级呈现，其他科目一般以“合格、不合格”呈现.若某省规定学业水平考试中历史科各等级人数所占比例依次为：A等级，B等级，C等级，D、E等级共.现采用分层抽样的方法，从某省参加历史学业水平考试的学生中抽取100人作为样本，则该样本中获得A或B等级的学生中一共有（ ）

    A.30人B.45人C.60人D.75人

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，过点作斜率为的直线交抛物线于两点.

    （1）若，求的面积；

    （2）过点分别作抛物线的两条切线，且直线与直线相交于点，问：点是否在某条定直线上？若在，求该定直线的方程；若不在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三棱柱中，侧棱底面， ， ， 是棱的中点.

    （Ⅰ）证明：平面平面；

    （Ⅱ）求平面与平面所成二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家电公司进行关于消费档次的调查，根据家庭年均家电消费额将消费档次分为4组：不超过3000元、超过3000元且不超过5000元、超过5000元且不超过10000元、超过10000元，从A、B两市中各随机抽取100个家庭，统计数据如下表所示：

    消费

    档次

    不超过3000元

    超过3000元

    且不超过5000元

    超过5000元

    且不超过10000元

    超过10000元

    A市

    20

    50

    20

    10

    B市

    50

    30

    10

    10

    年均家电消费额不超过5000元的家庭视为中低消费家庭，超过5000元的视为中高消费家庭.

    （1）从A市的100个样本中任选一个家庭，求此家庭属于中低消费家庭的概率；

    （2）现从A、B两市中各任选一个家庭，分别记为甲、乙，估计甲的消费档次不低于乙的消费档次的概率；

    （3）以各消费档次的区间中点对应的数值为该档次的家庭年均家电消费额，估计A、B两市中，哪个市的家庭年均家电消费额的方差较大（直接写出结果，不必说明理由）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某面包店推出一款新面包，每个面包的成本价为4元，售价为10元，该款面包当天只出一炉（一炉至少15个，至多30个），当天如果没有售完，剩余的面包以每个2元的价格处理掉.为了确定这一炉面包的个数，该店记录了这款新面包最近30天的日需求量（单位：个），整理得下表：

    日需求量

    15

    18

    21

    24

    27

    频数

    10

    8

    7

    3

    2

    （1）根据表中数据可知，频数与日需求量（单位：个）线性相关，求关于的线性回归方程；

    （2）以30天记录的各日需求量的频率代替各日需求量的概率，若该店这款新面包出炉的个数为24，记当日这款新面包获得的总利润为（单位：元）.

    （i）若日需求量为15个，求；

    （ii）求的分布列及其数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a，b，c分别为内角A，B，C的对边，且（2b﹣c）cosA＝acosC．

    （1）求A；

    （2）若△ABC的面积为，求a的最小值．

    查看答案和解析>>

    同步练习册答案