
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且(2b﹣c)cosA=acosC.
(1)求A;
(2)若△ABC的面积为![]() ,求a的最小值.
,求a的最小值.
【答案】(1)A![]() .(2)a的最小值为2.
.(2)a的最小值为2.
【解析】
(1)由正弦定理将(2b﹣c)cosA=acosC,转化为(2sinB﹣sinC)cosA=sinAcosC,再利用两角和的正弦公式求解.
(2)根据A![]() 和△ABC的面积为
和△ABC的面积为![]() bcsinA
bcsinA![]() bc,求得bc=4,由余弦定理得a2=b2+c2﹣2bccosA=b2+c2﹣bc,再利用基本不等式求解.
bc,求得bc=4,由余弦定理得a2=b2+c2﹣2bccosA=b2+c2﹣bc,再利用基本不等式求解.
(1)∵(2b﹣c)cosA=acosC,
∴由正弦定理可得:(2sinB﹣sinC)cosA=sinAcosC,
∴2sinBcosA=sinCcosA+sinAcosC=sin(A+C)=sinB,
∵sinB≠0,
∴cosA![]() ,
,
∵A∈(0,π),
∴A![]() .
.
(2)∵A![]() ,△ABC的面积为
,△ABC的面积为![]() bcsinA
bcsinA![]() bc,
bc,
∴bc=4,
∴a2=b2+c2﹣2bccosA=b2+c2﹣bc≥2bc﹣bc=bc=4,
解得a≥2,当且仅当b=c=2时等号成立,
∴a的最小值为2.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】现有若干扑克牌:6张牌面分别是2,3,4,5,6,7的扑克牌各一张,先后从中取出两张.若每次取后放回,连续取两次,点数之和是偶数的概率为![]() ;若每次取后不放回,连续取两次,点数之和是偶数的概率为
;若每次取后不放回,连续取两次,点数之和是偶数的概率为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.以上三种情况都有可能
D.以上三种情况都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,
为自然对数的底数,![]() .
.
(1)讨论函数![]() 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(2)已知![]() ,
,![]() ,若
,若![]() 对任意
对任意![]() 都成立,求
都成立,求![]() 的最大值;
的最大值;
(3)设![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为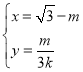 (
(![]() 为参数),设直线
为参数),设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时点
变化时点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生,则第3,4,5组抽取的学生人数依次为( )
,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生,则第3,4,5组抽取的学生人数依次为( )
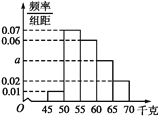
A.4,5,6B.3,2,1C.2,4,5D.2,1,3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,贵阳一中“保护饮用水源地”课题研究小组的同学们对红枫湖、百花湖、阿哈水库、花溪水库、北郊水库5处水源地进行了样本采集并送环保部门进行水质检测.已知5处水源地中有1处被某污染物污染,需要通过检测水源样本来确定被污染的水源地现有三个检測方案:
方案甲:对5个样本逐个检测,直到能确定被污染的水源地为止.
方案乙:先任取1个样本进行检测,若检测到污染物,则检测结束;若未检测到污染物,则在剩余4个样本中任取2个,并将这2个样本取部分混合在一起检测,若检测到污染物,则再在这2个样本中任取一个检测,否则在剩余2个未检测样本中任取一个检测.
方案丙:先任取2个样本,并将这2个样本取部分混合在一起检测,若检测到污染物,则再在这2个样本中任取一个检测;若未检测到污染物,则对剩余3个未检测样本进行逐个检测,直到能确定被污染的水源地为止.假设随机变量![]() 分别表示用方案甲、方案乙、方案丙进行检测所需的检测次数.
分别表示用方案甲、方案乙、方案丙进行检测所需的检测次数.
(1)求![]() 能取到的最大值和其对应的概率;
能取到的最大值和其对应的概率;
(2)求![]() 的期望假设每次检测的费用都相同,请从经济角度说明方案乙和方案丙哪一个更适合?
的期望假设每次检测的费用都相同,请从经济角度说明方案乙和方案丙哪一个更适合?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》 第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数y与月份之间的回归直线方程![]() +
+![]()
(2)预测该路口7月份的不“礼让斑马线”违章驾驶员人数;
(3)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查驾驶员不“礼让斑马线”行为与驾龄的关系,得到如下2![]() 列联表:
列联表:
不礼让斑马线 | 礼让斑马线 | 合计 | |
驾龄不超过1年 | 22 | 8 | 30 |
驾龄1年以上 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
能否据此判断有97.5![]() 的把握认为“礼让斑马线”行为与驾龄有关?
的把握认为“礼让斑马线”行为与驾龄有关?
参考公式及数据: ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() (其中n=a+b+c+d)
(其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
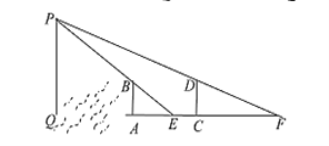
【题目】我国古代数学家刘徽在其《海岛算经》中给出了著名的望海岛问题及二次测望方法:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表三相直.从前表却行一百二十三步,人目着地取望岛峰,与表末三合.从后表却行一百二十七步,人目着地取望岛峰,亦与表末三合.问岛高及去表各几何?这一方法领先印度500多年,领先欧洲1300多年.其大意为:测量望海岛PQ的高度及海岛离岸距离,在海岸边立两根等高的标杆![]() (
(![]() 共面,均垂直于地面),使目测点E与P、B共线,目测点F与P、D共线,测出AE、CF、AC即可求出岛高和距离(如图).若
共面,均垂直于地面),使目测点E与P、B共线,目测点F与P、D共线,测出AE、CF、AC即可求出岛高和距离(如图).若![]() ,则
,则![]() ________;
________;![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com