
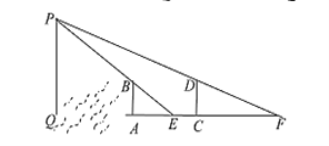
【题目】我国古代数学家刘徽在其《海岛算经》中给出了著名的望海岛问题及二次测望方法:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表三相直.从前表却行一百二十三步,人目着地取望岛峰,与表末三合.从后表却行一百二十七步,人目着地取望岛峰,亦与表末三合.问岛高及去表各几何?这一方法领先印度500多年,领先欧洲1300多年.其大意为:测量望海岛PQ的高度及海岛离岸距离,在海岸边立两根等高的标杆![]() (
(![]() 共面,均垂直于地面),使目测点E与P、B共线,目测点F与P、D共线,测出AE、CF、AC即可求出岛高和距离(如图).若
共面,均垂直于地面),使目测点E与P、B共线,目测点F与P、D共线,测出AE、CF、AC即可求出岛高和距离(如图).若![]() ,则
,则![]() ________;
________;![]() ______.
______.
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且(2b﹣c)cosA=acosC.
(1)求A;
(2)若△ABC的面积为![]() ,求a的最小值.
,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,某窑洞窗口形状上部是圆弧![]() ,下部是一个矩形
,下部是一个矩形![]() ,圆弧
,圆弧![]() 所在圆的圆心为O,经测量
所在圆的圆心为O,经测量![]() 米,
米,![]() 米,
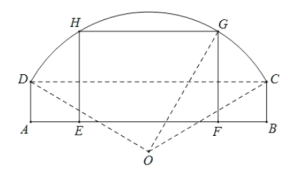
米,![]() ,现根据需要把此窑洞窗口形状改造为矩形
,现根据需要把此窑洞窗口形状改造为矩形![]() ,其中E,F在边
,其中E,F在边![]() 上,G,H在圆弧
上,G,H在圆弧![]() 上.设
上.设![]() ,矩形
,矩形![]() 的面积为S.
的面积为S.
(1)求矩形![]() 的面积S关于变量
的面积S关于变量![]() 的函数关系式;
的函数关系式;
(2)求![]() 为何值时,矩形
为何值时,矩形![]() 的面积S最大?
的面积S最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,且当n2时,![]()
(1)若=1,证明数列{a2n1}是等差数列;
(2)若=2.①设![]() ,求数列{bn}的通项公式;②设
,求数列{bn}的通项公式;②设![]() ,证明:对于任意的p,m N *,当p m,都有
,证明:对于任意的p,m N *,当p m,都有![]() Cm.
Cm.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且![]() ,
, ![]() .
.

求证:(1)直线DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
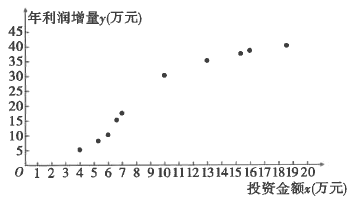
【题目】某果园种植“糖心苹果”已有十余年,为了提高利润,该果园每年投入一定的资金,对种植采摘包装宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额![]() (单位:万元)与年利润增量
(单位:万元)与年利润增量![]() (单位:万元)的散点图:
(单位:万元)的散点图:
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了![]() 关于
关于![]() 的两个回归模型;
的两个回归模型;
模型①:由最小二乘公式可求得![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() ;
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:![]() 的附近,对投资金额
的附近,对投资金额![]() 做交换,令
做交换,令![]() ,则
,则![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)分别利用这两个回归模型,预测投资金额为20万元时的年利润增量(结果保留两位小数);
(3)根据下列表格中的数据,比较两种模型的相关指数![]() ,并说明谁的预测值精度更高更可靠.
,并说明谁的预测值精度更高更可靠.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:样本![]() 的最小乘估计公式为
的最小乘估计公式为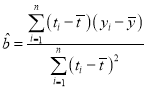 ,
,![]() ;
;
相关指数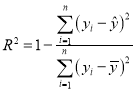 .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形且侧棱垂直与底面的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中,
的组合体中,![]() .
.
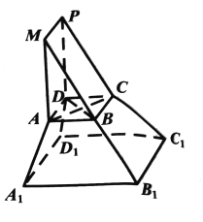
(1)证明:直线![]() 平面
平面![]() ;
;
(2)已知![]() ,且三棱锥A-A1B1D1的体积
,且三棱锥A-A1B1D1的体积![]() ,求该组合体的体积.
,求该组合体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上零点的个数;
上零点的个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com