
【题目】某果园种植“糖心苹果”已有十余年,为了提高利润,该果园每年投入一定的资金,对种植采摘包装宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额![]() (单位:万元)与年利润增量
(单位:万元)与年利润增量![]() (单位:万元)的散点图:
(单位:万元)的散点图:
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了![]() 关于
关于![]() 的两个回归模型;
的两个回归模型;
模型①:由最小二乘公式可求得![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() ;
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:![]() 的附近,对投资金额
的附近,对投资金额![]() 做交换,令
做交换,令![]() ,则
,则![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
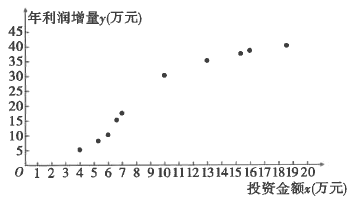
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)分别利用这两个回归模型,预测投资金额为20万元时的年利润增量(结果保留两位小数);
(3)根据下列表格中的数据,比较两种模型的相关指数![]() ,并说明谁的预测值精度更高更可靠.
,并说明谁的预测值精度更高更可靠.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:样本![]() 的最小乘估计公式为
的最小乘估计公式为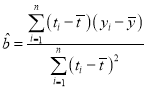 ,
,![]() ;
;
相关指数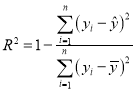 .
.
参考数据:![]() ,
,![]() .
.
【答案】(1)![]() .(2)
.(2)![]() (万元)(3)答案见解析
(万元)(3)答案见解析
【解析】
(1)根据题设中的数据和公式,求得![]() 的值,即可得到回归直线的方程;
的值,即可得到回归直线的方程;
(2)把![]() 时,代入回归直线的方程,即可求得求得模型①的年利润增量的预测值和模型②的年利润增量的预测值;
时,代入回归直线的方程,即可求得求得模型①的年利润增量的预测值和模型②的年利润增量的预测值;
(3)由![]() ,可得模型①的
,可得模型①的![]() 小于模型②,说明回归模型②刻画的拟合效果更好,得到结论.
小于模型②,说明回归模型②刻画的拟合效果更好,得到结论.
(1)由题意,知![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,
又由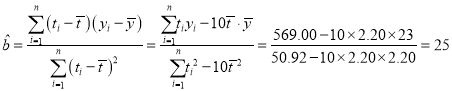 ,
,
则![]()
所以,模型②中![]() 关于
关于![]() 的回归方程
的回归方程![]() .
.
(2)当![]() 时,模型①的年利润增量的预测值为
时,模型①的年利润增量的预测值为![]() (万元),
(万元),
当![]() 时,模型②的年利润增量的预测值为
时,模型②的年利润增量的预测值为
![]() (万元),
(万元),
(3)由表格中的数据,可得![]() ,即
,即 ,
,
所以模型①的![]() 小于模型②,说明回归模型②刻画的拟合效果更好,
小于模型②,说明回归模型②刻画的拟合效果更好,
所以当![]() 时,模型②的预测值
时,模型②的预测值![]() 比模型①的预测值
比模型①的预测值![]() ,精度更高更可靠.
,精度更高更可靠.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念,贵阳一中“保护饮用水源地”课题研究小组的同学们对红枫湖、百花湖、阿哈水库、花溪水库、北郊水库5处水源地进行了样本采集并送环保部门进行水质检测.已知5处水源地中有1处被某污染物污染,需要通过检测水源样本来确定被污染的水源地现有三个检測方案:
方案甲:对5个样本逐个检测,直到能确定被污染的水源地为止.
方案乙:先任取1个样本进行检测,若检测到污染物,则检测结束;若未检测到污染物,则在剩余4个样本中任取2个,并将这2个样本取部分混合在一起检测,若检测到污染物,则再在这2个样本中任取一个检测,否则在剩余2个未检测样本中任取一个检测.
方案丙:先任取2个样本,并将这2个样本取部分混合在一起检测,若检测到污染物,则再在这2个样本中任取一个检测;若未检测到污染物,则对剩余3个未检测样本进行逐个检测,直到能确定被污染的水源地为止.假设随机变量![]() 分别表示用方案甲、方案乙、方案丙进行检测所需的检测次数.
分别表示用方案甲、方案乙、方案丙进行检测所需的检测次数.
(1)求![]() 能取到的最大值和其对应的概率;
能取到的最大值和其对应的概率;
(2)求![]() 的期望假设每次检测的费用都相同,请从经济角度说明方案乙和方案丙哪一个更适合?
的期望假设每次检测的费用都相同,请从经济角度说明方案乙和方案丙哪一个更适合?
查看答案和解析>>
科目:高中数学 来源: 题型:
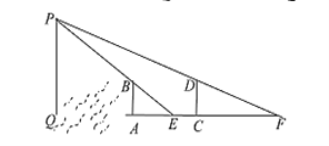
【题目】我国古代数学家刘徽在其《海岛算经》中给出了著名的望海岛问题及二次测望方法:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表三相直.从前表却行一百二十三步,人目着地取望岛峰,与表末三合.从后表却行一百二十七步,人目着地取望岛峰,亦与表末三合.问岛高及去表各几何?这一方法领先印度500多年,领先欧洲1300多年.其大意为:测量望海岛PQ的高度及海岛离岸距离,在海岸边立两根等高的标杆![]() (
(![]() 共面,均垂直于地面),使目测点E与P、B共线,目测点F与P、D共线,测出AE、CF、AC即可求出岛高和距离(如图).若
共面,均垂直于地面),使目测点E与P、B共线,目测点F与P、D共线,测出AE、CF、AC即可求出岛高和距离(如图).若![]() ,则
,则![]() ________;
________;![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示, ![]() 是边长为3的正方形,
是边长为3的正方形, ![]() 平面
平面![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)设点![]() 是线段
是线段![]() 上一个动点,试确定点
上一个动点,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,若存在一次函数
,若存在一次函数![]() ,使得对于任意的
,使得对于任意的![]() ,都有
,都有![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上的弱渐进函数.下列结论正确的是______.(写出所有正确命题的序号)
上的弱渐进函数.下列结论正确的是______.(写出所有正确命题的序号)
①![]() 是
是![]() 在
在![]() 上的弱渐进函数;
上的弱渐进函数;
②![]() 是
是![]() 在
在![]() 上的弱渐进函数;
上的弱渐进函数;
③![]() 是
是![]() 在
在![]() 上的弱渐进函数;
上的弱渐进函数;
④![]() 是
是![]() 在
在![]() 上的弱渐进函数.
上的弱渐进函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中取两个定点
中取两个定点![]() ,
,![]() ,再取两个动点
,再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(1)求直线![]() 与
与![]() 的交点
的交点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴且与轨迹
轴且与轨迹![]() 交于另一点
交于另一点![]() ,
,![]() 为轨迹
为轨迹![]() 的右焦点,若
的右焦点,若![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.

(1)用样本估计总体,以频率作为概率,若在![]() 两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: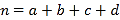 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com