
【题目】函数![]() 的定义域为
的定义域为![]() ,若存在一次函数
,若存在一次函数![]() ,使得对于任意的
,使得对于任意的![]() ,都有
,都有![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上的弱渐进函数.下列结论正确的是______.(写出所有正确命题的序号)
上的弱渐进函数.下列结论正确的是______.(写出所有正确命题的序号)
①![]() 是
是![]() 在
在![]() 上的弱渐进函数;
上的弱渐进函数;
②![]() 是
是![]() 在
在![]() 上的弱渐进函数;
上的弱渐进函数;
③![]() 是
是![]() 在
在![]() 上的弱渐进函数;
上的弱渐进函数;
④![]() 是
是![]() 在
在![]() 上的弱渐进函数.
上的弱渐进函数.
 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
【题目】若椭圆![]() 的离心率等于
的离心率等于![]() ,抛物线
,抛物线![]() 的焦点在椭圆
的焦点在椭圆![]() 的顶点上.
的顶点上.
(1)求抛物线![]() 的方程;
的方程;
(2)若过![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,又过
两点,又过![]() 、
、![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 、
、![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
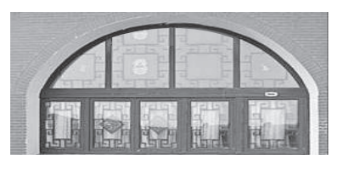
【题目】如下图所示,某窑洞窗口形状上部是圆弧![]() ,下部是一个矩形
,下部是一个矩形![]() ,圆弧
,圆弧![]() 所在圆的圆心为O,经测量
所在圆的圆心为O,经测量![]() 米,
米,![]() 米,
米,![]() ,现根据需要把此窑洞窗口形状改造为矩形
,现根据需要把此窑洞窗口形状改造为矩形![]() ,其中E,F在边
,其中E,F在边![]() 上,G,H在圆弧
上,G,H在圆弧![]() 上.设
上.设![]() ,矩形
,矩形![]() 的面积为S.
的面积为S.
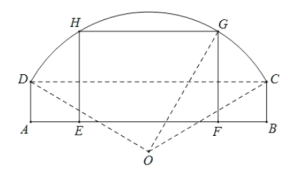
(1)求矩形![]() 的面积S关于变量
的面积S关于变量![]() 的函数关系式;
的函数关系式;
(2)求![]() 为何值时,矩形
为何值时,矩形![]() 的面积S最大?
的面积S最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且![]() ,
, ![]() .
.

求证:(1)直线DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某果园种植“糖心苹果”已有十余年,为了提高利润,该果园每年投入一定的资金,对种植采摘包装宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额![]() (单位:万元)与年利润增量
(单位:万元)与年利润增量![]() (单位:万元)的散点图:
(单位:万元)的散点图:
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了![]() 关于
关于![]() 的两个回归模型;
的两个回归模型;
模型①:由最小二乘公式可求得![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() ;
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:![]() 的附近,对投资金额
的附近,对投资金额![]() 做交换,令
做交换,令![]() ,则
,则![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
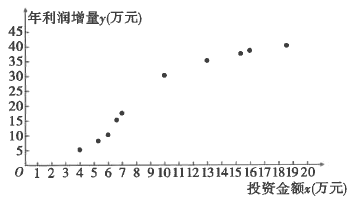
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)分别利用这两个回归模型,预测投资金额为20万元时的年利润增量(结果保留两位小数);
(3)根据下列表格中的数据,比较两种模型的相关指数![]() ,并说明谁的预测值精度更高更可靠.
,并说明谁的预测值精度更高更可靠.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:样本![]() 的最小乘估计公式为
的最小乘估计公式为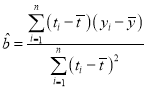 ,
,![]() ;
;
相关指数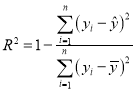 .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,是一个半圆柱与多面体![]() 构成的几何体,平面
构成的几何体,平面![]() 与半圆柱的下底面共面,且
与半圆柱的下底面共面,且![]() ,
, ![]() 为弧
为弧![]() 上(不与
上(不与![]() 重合)的动点.
重合)的动点.
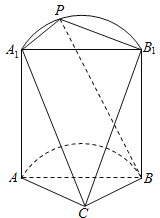
(1)证明: ![]() 平面
平面![]() ;
;
(2)若四边形![]() 为正方形,且
为正方形,且![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中将底面为直角三角形且侧棱垂直与底面的棱柱称为堑堵,将底面为矩形的棱台称为刍童.在如图所示的堑堵![]() 与刍童
与刍童![]() 的组合体中,
的组合体中,![]() .
.
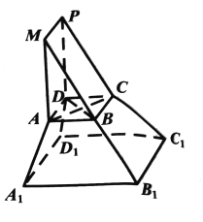
(1)证明:直线![]() 平面
平面![]() ;
;
(2)已知![]() ,且三棱锥A-A1B1D1的体积
,且三棱锥A-A1B1D1的体积![]() ,求该组合体的体积.
,求该组合体的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com