
【题目】已知数列{an}满足:a1=1,且当n2时,![]()
(1)若=1,证明数列{a2n1}是等差数列;
(2)若=2.①设![]() ,求数列{bn}的通项公式;②设
,求数列{bn}的通项公式;②设![]() ,证明:对于任意的p,m N *,当p m,都有
,证明:对于任意的p,m N *,当p m,都有![]() Cm.
Cm.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为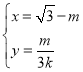 (
(![]() 为参数),设直线
为参数),设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时点
变化时点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,
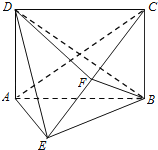
(1)求证:AE∥平面BDF;
(2)求证:平面BDF⊥平面ACE;
(3)2AE=EB,在线段AE上找一点P,使得二面角P﹣DB﹣F的余弦值为![]() ,求P的位置.
,求P的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() .
.
(1)证明:数列![]() 为等差数列;
为等差数列;
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,且对任意的正整数n,都有
,且对任意的正整数n,都有![]() ,求整数
,求整数![]() 的值;
的值;
(3)设数列![]() 满足
满足![]() ,若
,若![]() ,且存在正整数s,t,使得
,且存在正整数s,t,使得![]() 是整数,求
是整数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
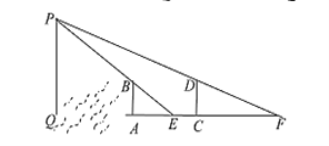
【题目】我国古代数学家刘徽在其《海岛算经》中给出了著名的望海岛问题及二次测望方法:今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表三相直.从前表却行一百二十三步,人目着地取望岛峰,与表末三合.从后表却行一百二十七步,人目着地取望岛峰,亦与表末三合.问岛高及去表各几何?这一方法领先印度500多年,领先欧洲1300多年.其大意为:测量望海岛PQ的高度及海岛离岸距离,在海岸边立两根等高的标杆![]() (
(![]() 共面,均垂直于地面),使目测点E与P、B共线,目测点F与P、D共线,测出AE、CF、AC即可求出岛高和距离(如图).若
共面,均垂直于地面),使目测点E与P、B共线,目测点F与P、D共线,测出AE、CF、AC即可求出岛高和距离(如图).若![]() ,则
,则![]() ________;
________;![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示, ![]() 是边长为3的正方形,
是边长为3的正方形, ![]() 平面
平面![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)设点![]() 是线段
是线段![]() 上一个动点,试确定点
上一个动点,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中取两个定点
中取两个定点![]() ,
,![]() ,再取两个动点
,再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(1)求直线![]() 与
与![]() 的交点
的交点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴且与轨迹
轴且与轨迹![]() 交于另一点
交于另一点![]() ,
,![]() 为轨迹
为轨迹![]() 的右焦点,若
的右焦点,若![]() ,求证:
,求证:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com