
【题目】已知数列![]() 满足
满足![]() .
.
(1)证明:数列![]() 为等差数列;
为等差数列;
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,且对任意的正整数n,都有
,且对任意的正整数n,都有![]() ,求整数
,求整数![]() 的值;
的值;
(3)设数列![]() 满足
满足![]() ,若
,若![]() ,且存在正整数s,t,使得
,且存在正整数s,t,使得![]() 是整数,求
是整数,求![]() 的最小值.
的最小值.
【答案】(1)证明见解析;(2)2;(3)![]()
【解析】
(1)令![]() 中的
中的![]() 为
为![]() ,又得一式,将两式做差变形,利用等差中项进行证明;
,又得一式,将两式做差变形,利用等差中项进行证明;
(2)利用放缩法和裂项相消法在数列求和中的应用进行证明.
(3)利用假设法的应用和存在性问题的应用求出最小值.
解:(1)因为![]() ①
①
所以![]() 时,
时,![]() ②
②
①-②得![]() ,
,
所以![]()
即![]()
所以数列![]() 为等差数列;
为等差数列;
(2)因为![]() ,所以
,所以![]() 的公差为1,
的公差为1,
因为对任意的正整数![]() ,都有
,都有![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 或2,
或2,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,这与题意矛盾,所以
,这与题意矛盾,所以![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,![]() 恒成立,
恒成立,
因为![]() ,
,
![]()
![]() ,
,
综上,![]() 的值为2.
的值为2.
(3)因为![]() ,所以
,所以![]() 的公差为
的公差为![]() ,
,
所以![]() ,
,
所以![]() ,
,
由题意,设存在正整数s,t,使得![]() ,
,![]() ,
,
则![]() ,即
,即![]() ,
,
因为![]() ,
,
所以![]() 是偶数,
是偶数,
所以![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
所以存在![]() ,
,
综上,![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中,AB=AC,A1C⊥BC1,AB1⊥BC1,D,E分别是AB1和BC的中点.
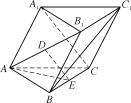
求证:(1)DE∥平面ACC1A1;
(2)AE⊥平面BCC1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F是抛物线C:y2=2px(p>0)的焦点,若点P(x0,4)在抛物线C上,且![]() .
.
(1)求抛物线C的方程;
(2)动直线l:x=my+1(m![]() R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
R)与抛物线C相交于A,B两点,问:在x轴上是否存在定点D(t,0)(其中t≠0),使得kAD+kBD=0,(kAD,kBD分别为直线AD,BD的斜率)若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”; ③“
”; ③“![]() ,则
,则![]() ”的否定是“
”的否定是“![]() ,则
,则![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题的个数是( )
”的充要条件.其中正确的命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为4.
,短轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条直线,分别交椭圆
作两条直线,分别交椭圆![]() 于
于![]() 两点(异于
两点(异于![]() ),当直线
),当直线![]() ,
,![]() 的斜率之和为4时,直线
的斜率之和为4时,直线![]() 恒过定点,求出定点的坐标.
恒过定点,求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,且当n2时,![]()
(1)若=1,证明数列{a2n1}是等差数列;
(2)若=2.①设![]() ,求数列{bn}的通项公式;②设
,求数列{bn}的通项公式;②设![]() ,证明:对于任意的p,m N *,当p m,都有
,证明:对于任意的p,m N *,当p m,都有![]() Cm.
Cm.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为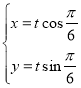 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)分别写出曲线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)P为曲线![]() 上的任意一点,过P向曲线
上的任意一点,过P向曲线![]() 引两条切线PA、PB,当
引两条切线PA、PB,当![]() 最大时,求P点的极坐标.
最大时,求P点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某果园种植“糖心苹果”已有十余年,根据其种植规模与以往的种植经验,产自该果园的单个“糖心苹果”的果径(最大横切面直径,单位:![]() )在正常环境下服从正态分布
)在正常环境下服从正态分布![]() .
.
(1)一顾客购买了20个该果园的“糖心苹果”,求会买到果径小于56![]() 的概率;
的概率;
(2)为了提高利润,该果园每年投入一定的资金,对种植、采摘、包装、宣传等环节进行改进.如图是2009年至2018年,该果园每年的投资金额![]() (单位:万元)与年利润增量
(单位:万元)与年利润增量![]() (单位:万元)的散点图:
(单位:万元)的散点图:
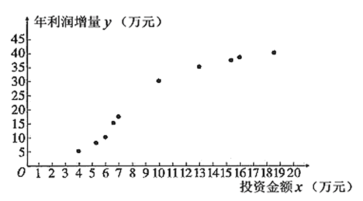
该果园为了预测2019年投资金额为20万元时的年利润增量,建立了![]() 关于
关于![]() 的两个回归模型;
的两个回归模型;
模型①:由最小二乘公式可求得![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() ;
;
模型②:由图中样本点的分布,可以认为样本点集中在曲线:![]() 的附近,对投资金额
的附近,对投资金额![]() 做交换,令
做交换,令![]() ,则
,则![]() ,且有
,且有![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测投资金额为20万元时的年利润增量(结果保留两位小数).
,并选择拟合精度更高、更可靠的模型,预测投资金额为20万元时的年利润增量(结果保留两位小数).
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附:若随机变量![]() ,则
,则![]() ,
,![]() ;样本
;样本![]() 的最小乘估计公式为
的最小乘估计公式为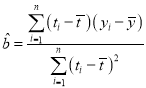 ,
,![]() ;
;
相关指数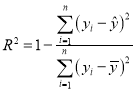 .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com