
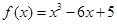 ,
,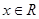
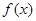 的单调区间;
的单调区间;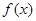 在区间
在区间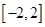 上的最值.
上的最值.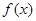 的单调递增区间为
的单调递增区间为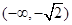 和
和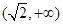 , 单调递减区间为
, 单调递减区间为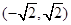 ;(Ⅱ)函数
;(Ⅱ)函数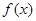 在区间
在区间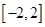 上的最大值为
上的最大值为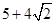 ,最小值为
,最小值为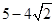 .
.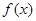 的单调区间,它的解题方法有两种:一是利用定义,二是导数法,本题由于是三次函数,可用导数法求单调区间,只需求出
的单调区间,它的解题方法有两种:一是利用定义,二是导数法,本题由于是三次函数,可用导数法求单调区间,只需求出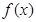 的导函数,判断
的导函数,判断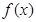 的导函数的符号,从而求出
的导函数的符号,从而求出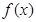 的单调区间;(Ⅱ)求函数
的单调区间;(Ⅱ)求函数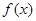 在区间
在区间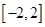 上的最值,求
上的最值,求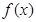 在区间
在区间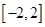 上的最大值,此题属于函数在闭区间上的最值问题,解此类题,只需求出极值,与端点处的函数值,比较谁大,就取谁,本题比较简单,属于送分题.
上的最大值,此题属于函数在闭区间上的最值问题,解此类题,只需求出极值,与端点处的函数值,比较谁大,就取谁,本题比较简单,属于送分题.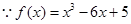 ,
,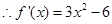 令
令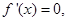
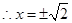
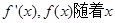 的变化情况如下表:
的变化情况如下表: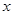 | 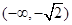 | 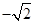 | 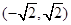 |  | 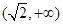 |
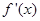 | 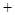 | 0 | — | 0 | 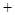 |
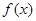 | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
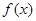 的单调递增区间为
的单调递增区间为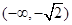 和
和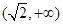 , 单调递减区间为
, 单调递减区间为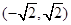 .
. 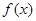 在
在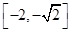 上单调递增,在
上单调递增,在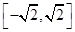 上单调递减,在
上单调递减,在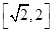 上单调递增,
上单调递增, 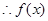 的极大值
的极大值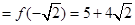 ,
, 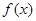 的极小值
的极小值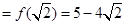
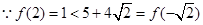 ,
, 
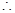 函数
函数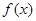 在区间
在区间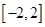 上的最大值为
上的最大值为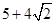 ,最小值为
,最小值为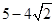 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:单选题
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com