
【题目】如图,三角形ABC的外接圆的O半径为![]() ,CD垂直于外接圆所在的平面,
,CD垂直于外接圆所在的平面, ![]()

(1)求证:平面![]()
![]() 平面
平面![]() .
.
(2)试问线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
【答案】(1)见解析;(2)满足条件的点M存在,且点M的坐标为![]() 。
。
【解析】试题分析:
(1)由题意结合几何关系可证得AC⊥BC,CD⊥BC,利用线面垂直的判断定理有BC⊥平面ACD,然后利用面面垂直的判断定理可得平面ADC![]() 平面BCDE
平面BCDE
(2)建立空间直角坐标系,结合题意可得满足条件的点M存在,且点M的坐标为![]() 。
。
试题解析:
(1)∵CD ⊥平面ABC,BE//CD
∴ BE⊥平面ABC,∴BE⊥AB
∵BE=1, ![]() ∴
∴ ![]() ,
,
从而![]()
∵⊙![]() 的半径为
的半径为![]() ,∴AB是直径,
,∴AB是直径,
∴AC⊥BC
又∵CD ⊥平面ABC,∴CD⊥BC,故BC⊥平面ACD
![]() 平面BCDE,∴平面ADC
平面BCDE,∴平面ADC![]() 平面BCDE
平面BCDE
(2)建立如图所示空间直角坐标系C—xyz,
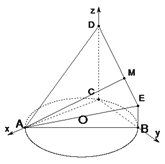
则:A(4,0,0),B(0,2,0),D(0,0,4),E(0,2,1),O(0,0,0),则![]()
易知平面ABC的法向量为![]() ,假设M点存在,设
,假设M点存在,设![]() ,则
,则![]() ,再设
,再设![]()
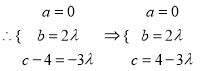 ,
,
即![]() ,从而
,从而![]() …10分
…10分
设直线BM与平面ABD所成的角为![]() ,则:
,则:
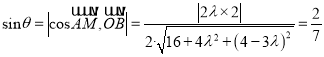
解得![]() ,其中
,其中![]() 应舍去,而
应舍去,而![]() 故满足条件的点M存在,且点M的坐标为
故满足条件的点M存在,且点M的坐标为![]()


科目:高中数学 来源: 题型:
【题目】如图,已知定圆![]() ,定直线
,定直线![]() ,过
,过![]() 的一条动直线
的一条动直线![]() 与直线相交于
与直线相交于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 中点.
中点.
(Ⅰ)当![]() 与
与![]() 垂直时,求证:
垂直时,求证:![]() 过圆心
过圆心![]() ;
;
(Ⅱ)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅲ)设![]() ,试问
,试问![]() 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出![]() 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,向量
,向量![]() ,
, ![]() ,经过点
,经过点![]() ,以
,以![]() 为方向向量的直线与经过点
为方向向量的直线与经过点![]() ,以
,以![]() 为方向向量的直线交于点
为方向向量的直线交于点![]() ,其中
,其中![]() .
.
(![]() )求点
)求点![]() 的轨迹方程,并指出轨迹
的轨迹方程,并指出轨迹![]() .
.
(![]() )若点
)若点![]() ,当
,当![]() 时,
时, ![]() 为轨迹
为轨迹![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,
时, ![]() 的零点为______;(将结果直接填写在横线上)
的零点为______;(将结果直接填写在横线上)
(Ⅱ)当![]() 时,如果存在
时,如果存在![]() ,使得
,使得![]() ,试求
,试求![]() 的取值范围;
的取值范围;
(Ⅲ)如果对于任意![]() ,都有
,都有![]() 成立,试求
成立,试求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在曲线![]() 上求一点,使它到直线
上求一点,使它到直线![]() :
: 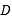 (
(![]() 为参数)的距离最短,写出
为参数)的距离最短,写出![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为![]() ,且点
,且点![]() 在该椭圆上。
在该椭圆上。
(I)求椭圆C的方程;
(II)过椭圆C的左焦点![]() 的直线l与椭圆C相交于
的直线l与椭圆C相交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求圆心在原点O且与直线l相切的圆的方程。
,求圆心在原点O且与直线l相切的圆的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com