
某地区为了绿化环境进行大面积植树造林,如图,在区域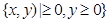 内植树,第一棵树在点Al(0,1),第二棵树在点.B1(l,l),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么
内植树,第一棵树在点Al(0,1),第二棵树在点.B1(l,l),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么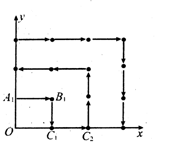
(1)第n棵树所在点坐标是(44,0),则n= .
(2)第2014棵树所在点的坐标是 .
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:填空题
已知双曲正弦函数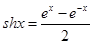 和双曲作弦函数
和双曲作弦函数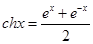 与我们学过的正弦函数和余弦函数有许多类似的性质,请类比正弦函数和余弦函数的和角或差角公式,写出双曲正弦或双曲余弦函数的一个类似的正确结论______________.
与我们学过的正弦函数和余弦函数有许多类似的性质,请类比正弦函数和余弦函数的和角或差角公式,写出双曲正弦或双曲余弦函数的一个类似的正确结论______________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
将全体正整数排成一个三角形数阵
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
… … … … … … … … …
根据以上排列规律,数阵中第 行的从左至右的第
行的从左至右的第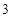 个数是 .
个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
观察下面两个推理过程及结论:
(1) 若锐角A, B, C满足A+B+C= , 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式:
, 以角A, B, C分别为内角构造一个三角形, 依据正弦定理和余弦定理可得到等式: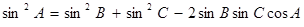
(2) 若锐角A, B, C满足A+B+C= , 则
, 则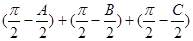 =
= , 以
, 以  分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
分别为内角构造一个三角形, 依据正弦定理和余弦定理可以
得到的等式: 则:若锐角A, B, C满
则:若锐角A, B, C满
足A+B+C= , 类比上面推理方法, 可以得到一个等式是 .
, 类比上面推理方法, 可以得到一个等式是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设f(x)是定义在实数集R上的函数,且满足f(x+2)=f(x+1)-f(x),如
果f(1)=lg ,f(2)=lg 15,则f(2 008)=________.
,f(2)=lg 15,则f(2 008)=________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得:
在y2=2px两边同时求导,得:
2yy'=2p,则y'=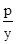 ,所以过P的切线的斜率:k=
,所以过P的切线的斜率:k=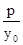 .
.
试用上述方法求出双曲线x2-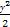 =1在P(
=1在P(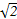 ,
,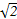 )处的切线方程为 .
)处的切线方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com