Question

（1）已知α、β、γ都是锐角，且tanα=,tanβ=,tanγ=,试求α+β+γ的值.

（2）求arctan1+arctan2+arctan3的值.

Answer 1

思路分析：对于第（1）小题可先求出tan（α+β）的值，再把α+β视为一个整体，求出tan［（α+β）+γ］的值，最后用反正切函数表示出α+β+γ的值；对于第（2）小题，由于arctan1=π[]4,所以只需求出arctan2+arctan3的值即可.

解：（1）∵tanα=,tanβ=,∴.

又∵tanγ=,

∴.

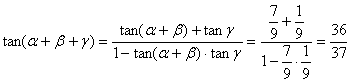∵α是锐角，且,∴0＜α＜.

同理，可得0＜β＜,0＜γ＜.

∴0＜α+β+γ＜.

∴α+β+γ=arctan.

（2）设arctan2=α,arctan3=β,

则tanα=2,tanβ=3且＜α＜,＜β＜.

∵,

又＜α+β＜π,∴α+β=,

即arctan2+arctan3=.

又arctan1=,∴arctan1+arctan2+arctan3=π.

方法归纳 已知三角函数值求角，需界定角的范围，为准确地求出所求的角，可根据三角函数的单调性，把所求的角放置于两个特殊角之间，以进一步缩小所求角的范围，避免增根的出现.