
(12分)连续抛两次质地均匀的骰子得到的点数分别为 和
和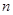 ,将
,将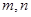 作为Q点的横、纵坐标,
作为Q点的横、纵坐标,
(1)记向量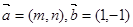 的夹角为
的夹角为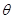 ,求
,求 的概率;
的概率;
(2)求点Q落在区域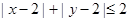 内的概率.
内的概率.
(1)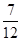 ;(2)
;(2)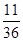 .
.
解析试题分析:(1)总的基本事件的个数有(1,1),(1,2),...,(6,6)共36个结果;
那么由于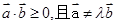 ,所以
,所以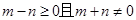 ,所以此事件包含的基本结果共有21个,
,所以此事件包含的基本结果共有21个,
所以此事件的概率为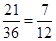 .
.
(2)作出不等式表示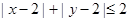 表示的平面区域可知是一个正方形,此正方形内包含横纵坐标都为正整数的点有11个,所以其概率为
表示的平面区域可知是一个正方形,此正方形内包含横纵坐标都为正整数的点有11个,所以其概率为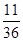 .
.
考点:向量的夹角,向量的数量积,线性规划,古典概型概率.
点评:根据向量夹角的范围可知向量的数量积大于零,据此可得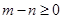 ,从而得到(1,1),(1,2),...(6,6)共36个点中有21个满足,然后根据古典概型概率计算公式计算即可.
,从而得到(1,1),(1,2),...(6,6)共36个点中有21个满足,然后根据古典概型概率计算公式计算即可.
第(2)问关键是正确作出不等式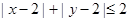 表示的平面区域可知是一个正方形,然后找出此正方形包括边上的整点个数,再根据古典概型概率计算公式计算即可.
表示的平面区域可知是一个正方形,然后找出此正方形包括边上的整点个数,再根据古典概型概率计算公式计算即可.


科目:高中数学 来源: 题型:解答题
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ,两人间每次射击是否击中目标互不影响。
,两人间每次射击是否击中目标互不影响。
(1)求乙至多击中目标2次的概率;
(2)求甲恰好比乙多击中目标1次的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
已知集合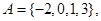 在平面直角坐标系中,点
在平面直角坐标系中,点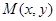 的横、纵坐标满足
的横、纵坐标满足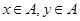 。
。
(1)请列出点 的所有坐标;
的所有坐标;
(2)求点 不在
不在 轴上的概率;
轴上的概率;
(3)求点 正好落在区域
正好落在区域 上的概率。
上的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ,命中得
,命中得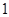 分,没有命中得
分,没有命中得 分;向乙靶射击两次,每次命中的概率为
分;向乙靶射击两次,每次命中的概率为 ,每命中一次得
,每命中一次得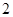 分,没有命中得
分,没有命中得 分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(1)求该射手恰好命中一次的概率;(2)求该射手的总得分
分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(1)求该射手恰好命中一次的概率;(2)求该射手的总得分 的分布列及数学期望
的分布列及数学期望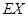 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)某网站欲调查网民对当前网页的满意程度,在登录的所有网民中,收回有效帖子共50000份,其中持各种态度的份数如下表所示.
| 很满意 | 满意 | 一般 | 不满意 |
| 10800 | 12400 | 15600 | 11200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一个盒子中,放有标号分别为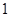 ,
,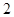 ,
, 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为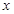 、
、 ,记
,记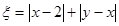 .
.
(Ⅰ)求随机变量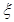 的最大值,并求事件“
的最大值,并求事件“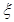 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量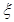 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com