
| A. | 6 | B. | -2$\sqrt{3}$ | C. | -6 | D. | 2$\sqrt{3}$ |
分析 由已知画出图形,然后利用向量的减法法则结合数量积运算求解得答案.
解答 解:∵$\overrightarrow{OA}$=$\overrightarrow{BC}$,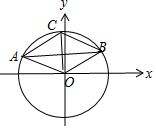
∴O、A、B、C构成平行四边形OABC,
∴$\overrightarrow{AC}=\overrightarrow{OB}$,$\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}$,
则$|\overrightarrow{OA}|=|\overrightarrow{OB}|=|\overrightarrow{OC}|=|\overrightarrow{BC}|=2$.
∴△BOC为等边三角形,∠BOC=60°,
则$\overrightarrow{AC}$•$\overrightarrow{BA}$=$\overrightarrow{OB}•(\overrightarrow{OA}-\overrightarrow{OB})=\overrightarrow{OB}•\overrightarrow{OA}-|\overrightarrow{OB}{|}^{2}$=$2×2×(-\frac{1}{2})-4=-6$.
故选:C.
点评 本题考查平面向量的数量积运算,考查了数学转化思想方法和数形结合的解题思想方法,属中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源:2017届江西南昌市新课标高三一轮复习训练五数学试卷(解析版) 题型:选择题
设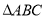 的内角
的内角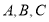 所对的边分别为
所对的边分别为 ,若
,若 ,则
,则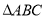 的形状为( )
的形状为( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,MA⊥平面ABCD,底面ABCD边长为1的正方形,MA=2AB,P是MC上一点,且$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$
如图所示,MA⊥平面ABCD,底面ABCD边长为1的正方形,MA=2AB,P是MC上一点,且$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
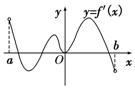 已知函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)上的图象如图所示,则函数f(x)在(a,b)上的极大值点的个数为( )
已知函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)上的图象如图所示,则函数f(x)在(a,b)上的极大值点的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
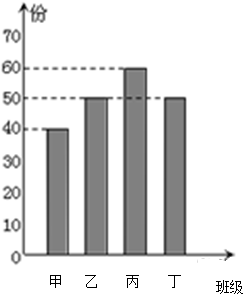 某研发公司研制出一款保护视力的护眼仪,并在新疆某中学的甲、乙、丙、丁四个班级中试用,这四个班级人数的条形图如下,为了了解学生护眼仪的使用情况,对四个班的学生进行了问卷调查,然后按分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
某研发公司研制出一款保护视力的护眼仪,并在新疆某中学的甲、乙、丙、丁四个班级中试用,这四个班级人数的条形图如下,为了了解学生护眼仪的使用情况,对四个班的学生进行了问卷调查,然后按分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:| 甲班 | 乙班 | 丙班 | 丁班 | |
| 满意 | 50% | 80% | 100% | 60% |
| 一般 | 25% | 0 | 0 | 0 |
| 不满意 | 25% | 20% | 0 | 40% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{3π}{4}$个单位 | D. | 向左平移$\frac{3π}{4}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com