
分析 由坐标原点为所求圆的圆心,且所求圆与已知直线垂直,利用点到直线的距离公式求出原点到已知直线的距离d,根据直线与圆相切时圆心到直线的距离等于圆的半径,即可得到所求圆的半径r,根据圆心和半径写出所求圆的方程即可;由两圆的圆心距为1,介于半径差与和之间,可得两圆相交.
解答 解:∵原点为所求圆的圆心,且所求圆与直线x+y+2=0相切,
∴所求圆的半径r=d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
则所求圆的方程为x2+y2=2.
x2+y2-2y-3=0的圆心为(0,1),半径为2,两圆的圆心距为1,介于半径差与和之间,两圆相交.
故答案为:x2+y2=2;相交.
点评 此题考查了直线与圆的位置关系,圆的标准方程,以及点到直线的距离公式,直线与圆的位置相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(文)试卷(解析版) 题型:解答题
在平面直角坐标系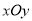 中,过点
中,过点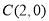 的直线与抛物线
的直线与抛物线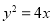 相交于点
相交于点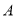 、
、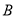 两点,设
两点,设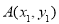 ,
,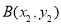 .
.
(1)求证: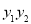 为定值;
为定值;
(2)是否存在平行于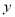 轴的定直线被以
轴的定直线被以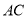 为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -2$\sqrt{3}$ | C. | -6 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{2}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
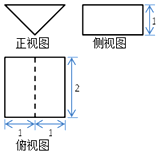 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com