
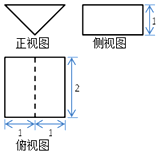
 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
科目:高中数学 来源: 题型:选择题
| A. | x2+y2=8 | B. | x2+y2=1 | C. | x2-y2=1 | D. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
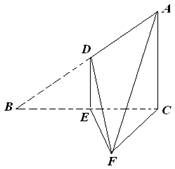 如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.
如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
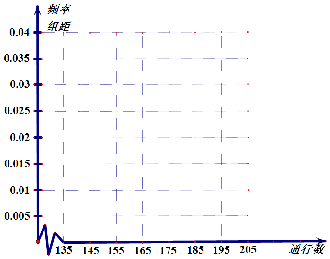 为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):
为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):| 通行数量区间 | [145,155) | [155,165) | [165,175) | [175,185) | [185,195) |
| 频数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com