
| A. | x2+y2=8 | B. | x2+y2=1 | C. | x2-y2=1 | D. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ |
分析 求出椭圆的标准方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$,F1(-2,0),F2(2,0),可设A(0,2),P(x,y),由已知条件求出x=y=2.从而得到点P的坐标一定满足x2+y2=8.
解答  解:∵椭圆x2+2y2=8的两个焦点分别为F1,F2,A为椭圆上的任意一点,
解:∵椭圆x2+2y2=8的两个焦点分别为F1,F2,A为椭圆上的任意一点,
∴椭圆的标准方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$,F1(-2,0),F2(2,0),
可设A(0,2),P(x,y),则$\overrightarrow{AP}$=(x,y-2),$\overrightarrow{A{F}_{2}}$=(2,-2),$\overrightarrow{{F}_{1}A}$=(2,2),$\overrightarrow{{F}_{2}P}$=(x-2,y),
∵AP是∠F1AF2的外角平分线,且$\overrightarrow{AP}•\overrightarrow{{F_2}P}=0$,
∴$\overrightarrow{AP}$•$\overrightarrow{{F}_{2}P}$=(x,y-2)•(x-2,y)=x2-2x+y2-2y=0,①
cos<$\overrightarrow{A{F}_{2}},\overrightarrow{AP}$>=cos<$\overrightarrow{{F}_{1}A}$,$\overrightarrow{AP}$>,即$\frac{2x-2y+4}{2\sqrt{2}•\sqrt{{x}^{2}+(y-2)^{2}}}$=$\frac{2x+2y-4}{2\sqrt{2}•\sqrt{{x}^{2}+(y-2)^{2}}}$,②
①②联立,解得x=y=2.
∴点P的坐标一定满足x2+y2=8.
故选:A.
点评 本题考查点的坐标满足的方程的确定的求法,是中档题,解题时要认真审题,注意椭圆、直线的性质的合理运用,注意特殊值法在选择题中的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{2}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
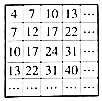 1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.
1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
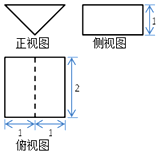 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com