
分析 (1)求出原函数的导函数,由题意可得f′(x)≥对任意x∈(1,4)恒成立,分离参数a,可得-a≤$\frac{(x+1)^{2}}{x}$,利用导数求出函数g(x)=$\frac{(x+1)^{2}}{x}$在(1,4)上的最小值得答案;
(2)设出切点坐标,求出函数在切点处的导数,可得切线斜率,再由两函数在切点处的函数值相等求得a的值.
解答 解:(1)函数f(x)=lnx+$\frac{ax}{x+1}$,
则f′(x)=$\frac{1}{x}+\frac{a}{(x+1)^{2}}$,
∵函数f(x)在区间(1,4)上单调递增,
∴$\frac{1}{x}+\frac{a}{(x+1)^{2}}$≥0在x∈(1,4)上恒成立.
即-a≤$\frac{(x+1)^{2}}{x}$在x∈(1,4)上恒成立.
令g(x)=$\frac{(x+1)^{2}}{x}$,则g′(x)=$\frac{{x}^{2}-1}{{x}^{2}}$.
当x∈(1,3)时,g′(x)>0,当x∈(3,4)时,g′(x)<0.
∴g(x)在(1,3)上为增函数,在(3,4)上为减函数,
∴g(x)min=g(1)=4.
则a≥-4;
(2)设切点坐标为(x0,y0),则f′(x0)=$\frac{1}{{x}_{0}}$+$\frac{a}{({x}_{0}+1)^{2}}$,
则$\frac{1}{{x}_{0}}$+$\frac{a}{({x}_{0}+1)^{2}}$=2
f(x0)=lnx0+$\frac{a{x}_{0}}{{x}_{0}+1}$=2x0,②
联立①,②解得:x0=1,a=4.
点评 本题考查利用导数研究函数的单调性,训练了恒成立问题的求解方法,考查计算能力,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | x2+y2=8 | B. | x2+y2=1 | C. | x2-y2=1 | D. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\sqrt{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | ±$\frac{\sqrt{3}}{2}$ | D. | ±1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,5} | B. | {3,4,5} | C. | {4,5} | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
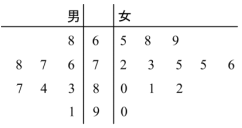 某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com