
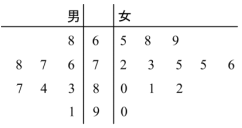
 某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.分析 (Ⅰ)由茎叶图能求出8名男生的平均成绩和12名女生成绩的中位数.
(Ⅱ)由茎叶图知,获“纪念奖”有有12人,获“优秀奖”的有8人,用分层抽样的方法从中抽取5人,则“纪念奖”抽取3人,“优秀奖”抽取2人,从这5人中选取3人,利用列举法能求出恰有1人获“优秀奖”的概率.
解答 解:(Ⅰ)8名男生的平均成绩为$\frac{68+76+77+78+83+84+87+91}{8}$=80.5,
12名女生成绩的中位数为75.
(Ⅱ)由茎叶图知,获“纪念奖”有有12人,获“优秀奖”的有8人,
用分层抽样的方法从中抽取5人,则“纪念奖”抽取12×$\frac{5}{20}$=3人,
“优秀奖”抽取2人,
从这5人中选取3人,基本事件总数n=${C}_{5}^{3}$=10,
恰有1人获“优秀奖”包含的基本事件个数m=${C}_{3}^{2}{C}_{2}^{1}$=6,
恰有1人获“优秀奖”的概率P=$\frac{m}{n}=\frac{6}{10}=\frac{3}{5}$.
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$+1 | C. | $\sqrt{2}$ | D. | 2+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinA)•sin2B>f(sinB)•sin2A | B. | f(sinA)•sin2B<f(sinB)•sin2A | ||
| C. | f(cosA)•sin2B>f(sinB)•cos2A | D. | f(cosA)•sin2B<f(sinB)•cos2A |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y+2)2=4 | B. | (x-2)2+(y+2)2=2 | C. | (x-2)2+(y+2)2=4 | D. | (x-2$\sqrt{2}$)2+(y+2$\sqrt{2}$)2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知定义在 内的函数
内的函数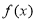 满足
满足 ,当
,当 时,
时,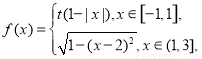 则当
则当 时,方程
时,方程 的不等实数根的个数是( )
的不等实数根的个数是( )
A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com