
分析 根据直线和圆相切的等价条件转化为圆心到直线的距离等于半径即可得到结论.
解答 解:圆心坐标为(0,0),半径为3,
∵点P(3,1)在圆外,
∴若直线斜率k不存在,
则直线方程为x=3,圆心到直线的距离为3,满足相切.
若直线斜率存在设为k,
则直线方程为y-1=k(x-3),即kx-y+1-3k=0,
则圆心到直线kx-y+1-3k=0的距离等于半径1,
即d=$\frac{|1-3k|}{\sqrt{{k}^{2}+1}}$=1,
解得k=-$\frac{4}{3}$,此时直线方程为4x+3y-15=0,
综上切线方程为x=3或4x+3y-15=0,
故答案为:x=3或4x+3y-15=0
点评 本题主要考查直线和圆的位置关系的应用,根据相切的等价条件是解决本题的关键.注意讨论直线的斜率是否存在.


科目:高中数学 来源: 题型:选择题
| A. | ±$\sqrt{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | ±$\frac{\sqrt{3}}{2}$ | D. | ±1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
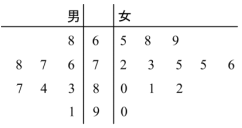 某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com