设函数且.则当时.的导函数的极小值为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

设函数且，则当时，的导函数的极小值为．

练习册系列答案

超能学典单元期中期末专题冲刺100分系列答案

期末100分冲刺卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

18．已知平面直角坐标系xOy中，过点P（-1，-2）的直线l的参数方程为$\left\{\begin{array}{l}{x=-1+tcos45°}\\{y=-2+tsin45°}\end{array}\right.$（t为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ•sinθ•tanθ=2a（a＞0），直线l与曲线C相交于不同的两点M、N．
（1）求曲线C的直角坐标方程和直线l的普通方程；
（2）若|PM|=|MN|，求实数a的值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

18．已知圆C：x²+y²=9，过点P（3，1）作圆C的切线，则切线方程为x=3或4x+3y-15=0．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

15．半径为2的圆C的圆心在第四象限，且与直线x=0和$x+y=2\sqrt{2}$均相切，则该圆的标准方程为（　　）

A．

（x-1）²+（y+2）²=4

B．

（x-2）²+（y+2）²=2

C．

（x-2）²+（y+2）²=4

D．

（x-2$\sqrt{2}$）²+（y+2$\sqrt{2}$）²=4

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．观察下列三角形数表：

假设第n行的第二个数为${a_n}（{n≥2，n∈{N^*}}）$，
（1）归纳出a_n+1与a_n的关系式，并求出a_n的通项公式；
（2）设a_nb_n=1（n≥2），求证：b₂+b₃+…+b_n＜2．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．已知{a_n}为等差数列，公差为d，且0＜d＜1，a₅≠$\frac{kπ}{2}$（k∈Z），sin²a₃+2sina₅•cosa₅=sin²a₇，函数f（x）=dsin（wx+4d）（w＞0）满足：在$x∈（0，\frac{3π}{4}）$上单调且存在${x_0}∈（0，\frac{3π}{4}），f（x）+f（2{x_0}-x）=0$，则w范围是0＜w≤$\frac{4}{3}$．．

查看答案和解析>>

科目：高中数学 来源：2017届湖南长沙长郡中学高三上周测十二数学（理）试卷（解析版） 题型：填空题

已知，满足约束条件若恒成立，则实数的取值范围为．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

13．

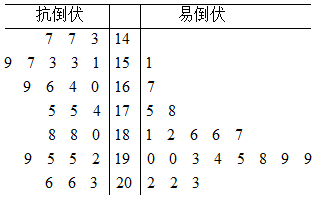为了打好脱贫攻坚战，某贫困县农科院针对玉米种植情况进行调研，力争有效地改良玉米品种，为农民提供技术支援．现对已选出的一组玉米的茎高进行统计，获得茎叶图如图（单位：厘米），设茎高大于或等于180厘米的玉米为高茎玉米，否则为矮茎玉米．
（1）完成2×2列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为抗倒伏与玉米矮茎有关？
（2）（i）按照分层抽样的方式，在上述样本中，从易倒伏和抗倒伏两组中抽出9株玉米，设取出的易倒伏矮茎玉米株数为X，求X的分布列（概率用组合数算式表示）
（ii）若将频率视为概率，从抗倒伏的玉米试验田中再随机取出50株，求取出的高茎玉米株数的数学期望和方差

P（K²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（ ${{K}^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．设双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦点分别为F₁，F₂，A为双曲线上的一点，且F₁F₂⊥AF₂，若直线AF₁与圆x²+y²=$\frac{{a}^{2}{+b}^{2}}{9}$相切，在双曲线的离心率为$\frac{\sqrt{2}+2\sqrt{6}}{4}$．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学