
| A. | f(sinA)•sin2B>f(sinB)•sin2A | B. | f(sinA)•sin2B<f(sinB)•sin2A | ||
| C. | f(cosA)•sin2B>f(sinB)•cos2A | D. | f(cosA)•sin2B<f(sinB)•cos2A |
分析 求出函数的导数,得到函数的单调性,从而判断出结论即可.
解答 解:∵${[\frac{f(x)}{{x}^{2}}]}^{′}$=$\frac{xf′(x)-2f(x)}{{x}^{3}}$,
x>0时,${[\frac{f(x)}{{x}^{2}}]}^{′}$>0,
∴$\frac{f(x)}{{x}^{2}}$在(0,+∞)递增,
又∵∠C是钝角,∴cosA>sinB>0,
∴$\frac{f(cosA)}{{cos}^{2}A}$>$\frac{f(sinB)}{{sin}^{2}B}$,
∴f(cosA)sin2B>f(sinB)cos2A,
故选:C.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | {2,4,5} | B. | {3,4,5} | C. | {4,5} | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=e为函数f(x)的极大值点 | B. | x=e为函数f(x)的极小值点 | ||
| C. | $x=\frac{1}{e}$为函数f(x)的极大值点 | D. | $x=\frac{1}{e}$为函数f(x)的极小值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
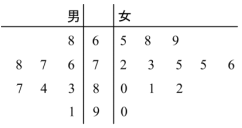 某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.
某学校举行物理竞赛,有8名男生和12名女生报名参加,将这20名学生的成绩制成茎叶图如图所示,成绩不低于80分的学生获得“优秀奖”,其余获“纪念奖”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,1,2} | B. | {-2,-1,1} | C. | {1} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在一个白球,它右侧的白球和黑球一样多 | |
| B. | 存在一个黑球,它右侧的白球和黑球一样多 | |
| C. | 存在一个白球,它右侧的白球比黑球少一个 | |
| D. | 存在一个黑球,它右侧的白球比黑球少一个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com