
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据题意和抛物线以及正三角形的对称性,可推断出两个边的斜率,进而表示出这两条直线,每条直线与抛物线均有两个交点,焦点两侧的两交点连接,分别构成一个等边三角形,可知当等边三角形关于x轴轴对称时,有两个.
解答 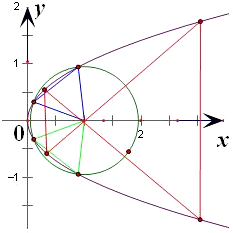 解:由题意,当等边三角形关于x轴轴对称时
解:由题意,当等边三角形关于x轴轴对称时
两个边的斜率k=±tan30°=±$\frac{\sqrt{3}}{3}$,其方程为:
y=±$\frac{\sqrt{3}}{3}$(x-4),
每条直线与抛物线均有两个交点,焦点两侧的两交点连接,分别构成一个等边三角形,这样的正三角形有2个,图中黑色的两个.
两个顶点同时在抛物线上方如图中蓝色,或同时在下方各一个如图中绿色,
故选D.
点评 本题主要考查了抛物线的简单性质和数形结合思想,主要是利用抛物线和正三角形的对称性.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | f(sinA)•sin2B>f(sinB)•sin2A | B. | f(sinA)•sin2B<f(sinB)•sin2A | ||
| C. | f(cosA)•sin2B>f(sinB)•cos2A | D. | f(cosA)•sin2B<f(sinB)•cos2A |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知定义在 内的函数
内的函数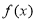 满足
满足 ,当
,当 时,
时,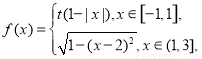 则当
则当 时,方程
时,方程 的不等实数根的个数是( )
的不等实数根的个数是( )
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
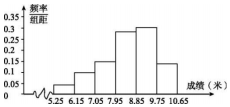 某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
不透明的袋子内装有相同的5个小球,分别标有1-5五个编号,现有放回的随机摸取三次,则摸出的三个小球的编号乘积能被10整除的概率为( )
A. B.
B.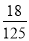
C. D.
D.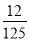
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com