
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 利用三角形以及向量关系,求解三角形的面积即可.
解答  解:由已知,在△ABC中,D为三角形所在平面内一点,
解:由已知,在△ABC中,D为三角形所在平面内一点,
且$\overrightarrow{AD}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$,
点D在平行于AB的中位线上,且为靠近AC边,
从而有${S_{△ABD}}=\frac{1}{2}{S_{△ABC}}$,${S_{△ACD}}=\frac{1}{3}{S_{△ABC}}$,
${S_{△BCD}}=(1-\frac{1}{2}-\frac{1}{3}){S_{△ABC}}=\frac{1}{6}{S_{△ABC}}$,有$\frac{{{S_{△BCD}}}}{{{S_{△ABD}}}}=\frac{1}{3}$.
故选:B.
点评 本题主要考查利用平面向量确定点的位置进而解决平几问题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在一个白球,它右侧的白球和黑球一样多 | |
| B. | 存在一个黑球,它右侧的白球和黑球一样多 | |
| C. | 存在一个白球,它右侧的白球比黑球少一个 | |
| D. | 存在一个黑球,它右侧的白球比黑球少一个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x 人数 y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
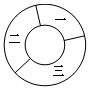 某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:解答题
已知集合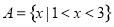 ,集合
,集合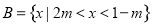 .
.
(1)当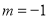 时,求
时,求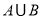 ;
;
(2)若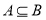 ,求实数
,求实数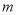 的取值范围;
的取值范围;
(3)若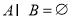 ,求实数
,求实数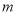 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com