
| x ���� y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
���� ��1����Ƶ��=$\frac{Ƶ��}{����}$�������a��b��ֵ��
��2����14+a+28��10+b+34����a��b+2���ɴ������оٷ������������ʣ�
��� �⣺��1����Ƶ��=$\frac{Ƶ��}{����}$���õ�$\frac{14}{n}=0.07$��
���n=200��
��$\frac{14+a+28}{200}=0.3$�����a=18��
��14+a+28+40+36+8+10+b+34=200��
��b=12��
��2����a+b=30����a��8��b��6��
����14+a+28��10+b+34����a��b+2��
��a��b�������н��Ϊ��8��22������9��21������10��20������11��19������12��18������13��17����
��14��16������15��15������16��14������17��12������18��12������19��20������20��10������21��9������22��8������23��7������24��6����
��17�飬
����a��b+2����8�飬
����ѧ�ɼ�ΪA�ȼ���������C�ȼ���������ĸ���P=$\frac{8}{17}$��
���� ���⿼��Ƶ�ʷֲ�����Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $\sqrt{5}$+1 | C�� | $\sqrt{2}$ | D�� | 2+$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-1��2+��y+2��2=4 | B�� | ��x-2��2+��y+2��2=2 | C�� | ��x-2��2+��y+2��2=4 | D�� | ��x-2$\sqrt{2}$��2+��y+2$\sqrt{2}$��2=4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����ϳ�ɳ������ѧ�������ܲ�ʮ����ѧ�������Ծ��������棩 ���ͣ������
��֪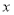 ��
��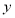 ����Լ������
����Լ������ ��
��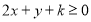 ���������ʵ��
���������ʵ��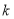 ��ȡֵ��ΧΪ ��
��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
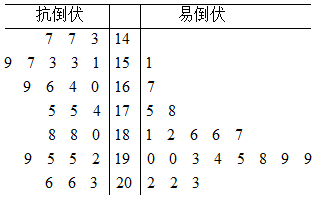 Ϊ�˴����ƶ����ս��ijƶ����ũ��Ժ���������ֲ������е��У�������Ч�ظ�������Ʒ�֣�Ϊũ���ṩ����֧Ԯ���ֶ���ѡ����һ�����ľ��߽���ͳ�ƣ���þ�Ҷͼ��ͼ����λ�����ף����辥�ߴ��ڻ����180��������Ϊ�߾����ף�����Ϊ�������ף�
Ϊ�˴����ƶ����ս��ijƶ����ũ��Ժ���������ֲ������е��У�������Ч�ظ�������Ʒ�֣�Ϊũ���ṩ����֧Ԯ���ֶ���ѡ����һ�����ľ��߽���ͳ�ƣ���þ�Ҷͼ��ͼ����λ�����ף����辥�ߴ��ڻ����180��������Ϊ�߾����ף�����Ϊ�������ף�| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����ϳ�ɳ������ѧ�������ܲ�ʮ����ѧ�������Ծ��������棩 ���ͣ�ѡ����
��֪������ �ڵĺ���
�ڵĺ���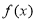 ����
���� ����
���� ʱ��
ʱ��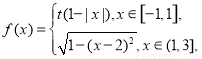 ��
�� ʱ������
ʱ������ �IJ���ʵ�����ĸ����ǣ� ��
�IJ���ʵ�����ĸ����ǣ� ��
A��3 B��4 C��5 D��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����ϳ�ɳ������ѧ�������ܲ�ʮ����ѧ�������Ծ��������棩 ���ͣ�ѡ����
�輯��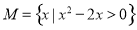 ������
������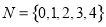 ����
����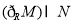 ���ڣ� ��
���ڣ� ��
A�� B��
B��
C��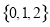 D��
D��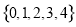
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com