
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
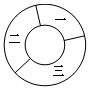 某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{10}$ | B. | $\frac{2π}{5}$ | C. | -$\frac{π}{10}$ | D. | -$\frac{2π}{5}$ |
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:解答题
已知集合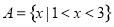 ,集合
,集合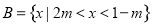 .
.
(1)当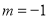 时,求
时,求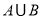 ;
;
(2)若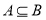 ,求实数
,求实数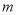 的取值范围;
的取值范围;
(3)若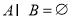 ,求实数
,求实数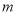 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com