
分析 (Ⅰ)【解法一】:求f(x)的导数f′(x),利用判别式△=a2-4,判断f′(x)是否大于0,
从而得出f(x)的单调性与极值点情况;
【解法二】:求f(x)的导数f′(x),根据x>0求出f'(x)的值域,
讨论a的值得出f′(x)的正负情况,判断f(x)的单调性和极值点问题;
(Ⅱ)( i)f(x)≤g(x)等价于ex-lnx+x2≥ax,
由x>0,利用分离常数法求出a的表达式,再构造函数求最值即可证明;
( ii)由( i)结论,a=e+1时有f(x)≤g(x),
得出不等式,再进行等价转化,证明转化的命题成立即可.
解答 解:(Ⅰ)【解法一】:由题意得$f'(x)=x+\frac{1}{x}+a=\frac{{{x^2}+ax+1}}{x}(x>0)$,令△=a2-4,
(1)当△=a2-4≤0,即-2≤a≤2时,x2+ax+1≥0对x>0恒成立;
即$f'(x)=\frac{{{x^2}+ax+1}}{x}≥0$对x>0恒成立,
此时f(x)没有极值点;…(2分)
(2)当△=a2-4>0,即a<-2或a>2,
①a<-2时,设方程x2+ax+1=0两个不同实根为x1,x2,不妨设x1<x2,
则x1+x2=-a>0,x1x2=1>0,故x2>x1>0,
∴x<x1或x>x2时f(x)>0;
在x1<x<x2时f(x)<0,
故x1,x2是函数f(x)的两个极值点;
②当a=-2时,△=0,函数f(x)有一个极值点;
③a>2时,设方程x2+ax+1=0两个不同实根为x1,x2,
则x1+x2=-a<0,x1x2=1>0,故x2<0,x1<0,
∴x>0时,f(x)>0;
故函数f(x)没有极值点;…(4分)
综上,a<-2时,函数f(x)有两个极值点;
a=-2时,函数f(x)有一个极值点;
a>-2时,函数f(x)没有极值点;…(5分)
【解法二】:由题意得$f'(x)=x+\frac{1}{x}+a$,…(1分)
∵x>0,∴f'(x)∈[a+2,+∞),
①当a+2≥0,即a∈[-2,+∞)时,f′(x)≥0对?x>0恒成立,
∴f(x)在(0,+∞)上单调递增,f(x)没有极值点; …(3分)
②当a+2<0,即a∈(-∞,-2)时,方程x2+ax+1=0有两个不等正数解x1,x2,
$f'(x)=x+\frac{1}{x}+a=\frac{{{x^2}+ax+1}}{x}=\frac{{(x-{x_1})(x-{x_2})}}{x}(x>0)$
不妨设0<x1<x2,则当x∈(0,x1)时,f'(x)>0,f(x)单调递增;
x∈(x1,x2)时,f'(x)<0,f(x)单调递减;
x∈(x2,+∞)时,f'(x)>0,f(x)单调递增,
所以x1,x2分别为f(x)极大值点和极小值点,f(x)有两个极值点.
综上所述,当a∈(-2,+∞)时,f(x)没有极值点;
当a=-2时,函数f(x)有一个极值点;
当a∈(-∞,-2)时,f(x)有两个极值点;…(5分)
(Ⅱ)( i)f(x)≤g(x)等价于ex-lnx+x2≥ax,
由x>0,即$a≤\frac{{{e^x}+{x^2}-lnx}}{x}$对于?x>0恒成立,
设$φ(x)=\frac{{{e^x}+{x^2}-lnx}}{x}(x>0)$,
$φ'(x)=\frac{{({e^x}+2x-\frac{1}{x})x-({e^x}+{x^2}-lnx)}}{x^2}=\frac{{{e^x}(x-1)+lnx+(x+1)(x-1)}}{x^2}$,
∵x>0,∴x∈(0,1)时,φ'(x)<0,φ(x)单调递减,
x∈(1,+∞)时,φ'(x)>0,φ(x)单调递增,
∴φ(x)≥φ(1)=e+1,∴a≤e+1; …(9分)
( ii)由( i)知,当a=e+1时有f(x)≤g(x),
即:${e^x}+\frac{3}{2}{x^2}≥lnx+\frac{1}{2}{x^2}+(e+1)x$,
等价于ex+x2-(e+1)x≥lnx…①当且仅当x=1时取等号,…(10分)
以下证明:$lnx+\frac{e}{x}≥2$,
设$θ(x)=lnx+\frac{e}{x}$,则$θ'(x)=\frac{1}{x}-\frac{e}{x^2}=\frac{x-e}{x^2}$,
∴当x∈(0,e)时θ'(x)<0,θ(x)单调递减,
x∈(e,+∞)时θ'(x)>0,θ(x)单调递增,
∴θ(x)≥θ(e)=2,
∴$lnx+\frac{e}{x}≥2$,…②当且仅当x=e时取等号;
由于①②等号不同时成立,故有${e^x}+{x^2}-(e+1)x+\frac{e}{x}>2$.…(12分)
点评 本题考查了函数与导数的综合应用问题,也考查了求函数最值与不等式恒成立问题,是综合性问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y+2)2=4 | B. | (x-2)2+(y+2)2=2 | C. | (x-2)2+(y+2)2=4 | D. | (x-2$\sqrt{2}$)2+(y+2$\sqrt{2}$)2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
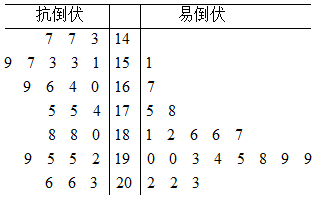 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知定义在 内的函数
内的函数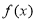 满足
满足 ,当
,当 时,
时,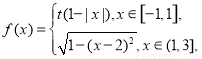 则当
则当 时,方程
时,方程 的不等实数根的个数是( )
的不等实数根的个数是( )
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{5}$ | C. | 2+2$\sqrt{3}$ | D. | $\sqrt{7}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com