
分析 由已知及基本不等式可求ab≤1,当且仅当a=b时取等号,当ab取得最大值时,由余弦定理可求cosC,利用同角三角函数基本关系式可求sinC,进而利用三角形面积公式即可计算得解.
解答 解:∵(a+b-c)(a+b+c)=ab,c=$\sqrt{3}$,
∴(a+b)2-c2=ab,可得:a2+b2=c2-ab=3-ab,
∵a2+b2≥2ab,当且仅当a=b时取等号,
∴3-ab≥2ab,即:ab≤1,当且仅当a=b时取等号,
∴当ab取得最大值时,a=b=1,可得:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$,sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{\sqrt{3}}{2}$,
可得:S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}×1×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$.
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题主要考查了基本不等式,余弦定理,同角三角函数基本关系式,三角形面积公式在解三角形中的应用,考查了转化思想,属于基础题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
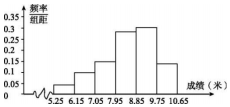 某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
不透明的袋子内装有相同的5个小球,分别标有1-5五个编号,现有放回的随机摸取三次,则摸出的三个小球的编号乘积能被10整除的概率为( )
A. B.
B.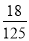
C. D.
D.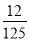
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
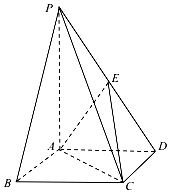 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com