
 为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):
为了摸清整个江门大道的交通状况,工作人员随机选取20处路段,在给定的测试时间内记录到机动车的通行数量情况如下(单位:辆):| 通行数量区间 | [145,155) | [155,165) | [165,175) | [175,185) | [185,195) |
| 频数 |
分析 (I)利用已知数据即可得出;
(II)用分层抽样的方法抽取7处,即可得出.利用P(X=k)=$\frac{{∁}_{4}^{k}{∁}_{3}^{2-k}}{{∁}_{7}^{2}}$,即可得出.
解答 解:(Ⅰ)
| 通行数量区间 | [145,155) | [155,165) | [165,175) | [175,185) | [185,195) |
| 频数 | 2 | 4 | 8 | 4 | 2 |

| X | 0 | 1 | 2 |
| P | $\frac{1}{7}$ | $\frac{4}{7}$ | $\frac{2}{7}$ |
点评 本题考查了频率分布直方图的性质、分层抽样方法、超几何分布列与数学期望计算公式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 方案 | a | b | c | d |
| 一 | 100 | 100 | 100 | 500 |
| 二 | 100 | 100 | 500 | 500 |
| 三 | 200 | 200 | 400 | 400 |
| 方案二 | 方案三 | 合计 | |
| 男性 | 12 | 48 | 60 |
| 女性 | 6 | 34 | 40 |
| 合计 | 18 | 82 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 |
| k0 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
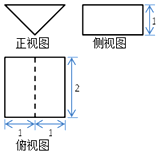 《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )
《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图,则它的表面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [0,+∞) | C. | (1,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
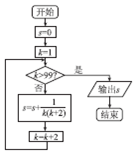
| A. | $\frac{49}{99}$ | B. | $\frac{50}{101}$ | C. | $\frac{51}{103}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12π | B. | $\frac{32}{3}$π | C. | 8π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com