Question

7．如图，在正方形ABCD中，E为BC边中点，若$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$，则λ+μ=$\frac{3}{2}$．

Answer 1

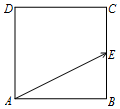
分析 利用正方形的性质、向量三角形法则、平面向量基本定理即可得出．

解答 解：∵$\overrightarrow{AD}=\overrightarrow{BC}$，
∴$\overrightarrow{AE}$=$\overrightarrow{AB}$+$\overrightarrow{BE}$=$\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{BC}$=$\overrightarrow{AB}$$+\frac{1}{2}\overrightarrow{AD}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$，
∴λ=1，$μ=\frac{1}{2}$．
则λ+μ=$\frac{3}{2}$．
故答案为：$\frac{3}{2}$．

点评 本题考查了正方形的性质、向量三角形法则、平面向量基本定理，考查了推理能力与计算能力，属于中档题．