练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．长方体长，宽，高分别为3，2，$\sqrt{3}$，则长方体的外接球体积为（　　）
    A．12πB．$\frac{32}{3}$πC．8πD．4π

    分析 长方体的对角线就是外接球的直径，求出长方体的对角线长，即可求出球的半径，外接球的体积可求．

    解答 解：由题意长方体的对角线就是球的直径．
    长方体的对角线长为：$\sqrt{9+4+3}$=4
    外接球的体积V=$\frac{4}{3}π•{2}^{3}$=$\frac{32}{3}π$
    故选B．

    点评 本题是基础题，考查长方体的外接球．关键是长方体的对角线就是外接球的直径．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．以椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的中心O为圆心，以$\sqrt{\frac{ab}{2}}$为半径的圆称为该椭圆的“伴随”．
    （1）若椭圆C的离心率为$\frac{\sqrt{3}}{2}$，其“伴随”与直线$\sqrt{3}$x+y-2=0相切，求椭圆C的方程．
    （2）设椭圆E：$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{4{b}^{2}}$=1，P为椭圆C上任意一点，过点P的直线y=kx+m交椭圆E于AB两点，射线PO交椭圆E于点Q．
    （i）求$\frac{|OQ|}{|OP|}$的值；
    （ii）求△ABQ面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

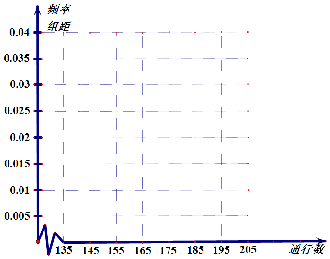    20．为了摸清整个江门大道的交通状况，工作人员随机选取20处路段，在给定的测试时间内记录到机动车的通行数量情况如下（单位：辆）：
    147  161  170  180  163  172  178  167  191  182
    181  173  174  165  158  154  159  189  168  169
    （Ⅰ）完成如下频数分布表，并作频率分布直方图；
    通行数量区间[145，155）[155，165）[165，175）[175，185）[185，195）
    频数
    （Ⅱ）现用分层抽样的方法从通行数量区间为[165，175）、[175，185）及[185，195）的路段中取出7处加以优化，再从这7处中随机选2处安装智能交通信号灯，设所取出的7处中，通行数量区间为[165，175）路段安装智能交通信号灯的数量为随机变量X（单位：盏），试求随机变量X的分布列与数学期望E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知集合A={x|-1＜x＜3}，B={x|x＜a}，若A∩B=A，则实数a的取值范围是（　　）
    A．a＞3B．a≥3C．a≥-1D．a＞-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=ax+lnx（a∈R）．
    （Ⅰ）若a=2，求曲线y=f（x）在x=1处的切线方程；
    （Ⅱ）求f（x）的单调区间；
    （Ⅲ）若对任意x∈（0，+∞），都有f（x）＜2成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．若实数x，y满足约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$，则目标函数z=3x+y的最大值为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设全集U=A∪B={1，2，3，4，5}，A∩（∁UB）={1，2}，则集合B=（　　）
    A．{2，4，5}B．{3，4，5}C．{4，5}D．（2，4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．函数f（x）=$\sqrt{3}$cos（3x-θ）-sin（3x-θ）是奇函数，则tanθ等于-$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．函数$f（x）=\frac{lnx}{x}$，则（　　）
    A．x=e为函数f（x）的极大值点B．x=e为函数f（x）的极小值点
    C．$x=\frac{1}{e}$为函数f（x）的极大值点D．$x=\frac{1}{e}$为函数f（x）的极小值点

    查看答案和解析>>

    同步练习册答案