
分析 (1)依题意,|x-1|+|x-2|≥2,通过对x的范围分类讨论,去掉绝对值符号,转化为一次不等式来解即可;
(2)利用分段函数y=|x-1|+|x-2|,根据绝对值的意义,可求得ymin,只需a≤ymin即可求得实数a的取值范围
解答 解:(1)f(x+2)≥2?|x+1|+|x|≥2,
当x≤-1时,不等式化为-2x-1≥2,解得:x≤-$\frac{3}{2}$;
当-1<x≤0时,不等式化为x+1-x≥2,无解;
当x>0时,不等式化为x+1+x≥2,解得:x≥$\frac{1}{2}$;
∴f(x+2)≥2的解集是{x|x≤-$\frac{3}{2}$或x≥$\frac{1}{2}$};
(2)由题意得:a≤f(x)min,
由f(x)=|x-1|+|x-2|≥|(x-1)-(x-2)|=1,
当且仅当(x-1)(x-2)≤0即x∈[1,2]取得最小值,
∴a≤1.
点评 本题考查绝对值不等式的解法,通过对x的范围分类讨论,去掉绝对值符号是解决问题的关键,属于中档题.


科目:高中数学 来源:2017届江西南昌市新课标高三一轮复习训练五数学试卷(解析版) 题型:选择题
“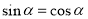 ”是“
”是“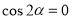 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,3,则输出v的值为48.
秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,3,则输出v的值为48.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{2}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
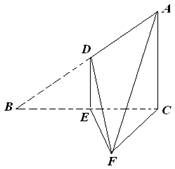 如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.
如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com