
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(理)试卷(解析版) 题型:选择题
已知集合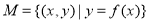 ,若对于任意
,若对于任意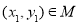 ,存在
,存在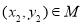 ,使得
,使得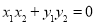 成立,则称集合
成立,则称集合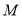 是“理想集合”.给出下列5个集合:
是“理想集合”.给出下列5个集合:
①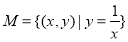 ;
;
②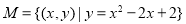 ;
;
③ ;
;
④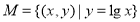 ;
;
⑤ .
.
其中所有“理想集合”的序号是( )
A.①② B.③⑤ C.②③⑤ D.③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$-2{e}^{-\frac{3}{2}}$) | B. | (-∞,1] | C. | (-2,0)∪(0,1] | D. | (-∞,$-2{e}^{-\frac{3}{2}}$]∪{1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
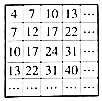 1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.
1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com