
分析 (1)求导f′(x)=(x-m+1)ex,切线的斜率k=-$\frac{1}{2}$,故f′(0)=1-m=-$\frac{1}{2}$,解得:m=$\frac{3}{2}$;
(2)f′(x)=(x-m+1)ex,f′(x)>0,求得函数的单调递增区间,f′(x)<0,求得函数函数的单调递减区间;
(3)当m=0时,f(x)=xex,设g(x)=xex-lnx-x-1,(x>0),求导g′(x)=(x+1)(ex-$\frac{1}{x}$),利用基本初等函数的单调性,求得g(x)单调性,g(x)≥g(x0)=x0(${e}^{{x}_{0}}$-$\frac{1}{{x}_{0}}$)-lnx0-x0=0,即可证明,f(x)≥lnx+x+1.
解答 解:(1)函数f(x)=(x-m)ex,求导f′(x)=(x-m+1)ex,
若f(x)在原点处的切线与y=2x+1垂直,则切线的斜率k=-$\frac{1}{2}$,
故f′(0)=1-m=-$\frac{1}{2}$,
解得:m=$\frac{3}{2}$;
(2)f′(x)=(x-m+1)ex,
令f′(x)>0,解得:x>m-1,
令f′(x)<0,解得:x<m-1,
故f(x)在(-∞,m-1)递减,在(m-1,+∞)递增;
(3)证明:m=0时,f(x)=xex,
令g(x)=xex-lnx-x-1,(x>0),
g′(x)=(x+1)(ex-$\frac{1}{x}$),
由函数y=ex,在(0,+∞)上是增函数,函数y=$\frac{1}{x}$在(0,+∞)上是减函数,
则h(x)=ex-$\frac{1}{x}$在(0,+∞)上是增函数,则h($\frac{1}{2}$)=$\sqrt{e}$-2<0,h(1)=e-1>0,
∴函数h(x)存在零点,设零点为x0,${e}^{{x}_{0}}-\frac{1}{{x}_{0}}=0$,
∴lnx0+x0=0,
∴当0<x<x0,g′(x)<0,当x>x0,g′(x)>0,
故g(x)在(0,x0)上是减函数,在(x0,+∞)上是增函数,
∴g(x)≥g(x0)=x0(${e}^{{x}_{0}}$-$\frac{1}{{x}_{0}}$)-lnx0-x0=0,
∴f(x)≥lnx+x+1,
综上可知:函数f(x)≥lnx+x+1..
点评 本题考查导数的综合应用,考查导数的几何意义,利用导数求函数的单调性及最值,考查构造法,考查计算能力,属于中档题.


科目:高中数学 来源:2017届江西南昌市新课标高三一轮复习训练五数学试卷(解析版) 题型:选择题
“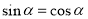 ”是“
”是“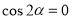 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,MA⊥平面ABCD,底面ABCD边长为1的正方形,MA=2AB,P是MC上一点,且$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$
如图所示,MA⊥平面ABCD,底面ABCD边长为1的正方形,MA=2AB,P是MC上一点,且$\overrightarrow{CP}$=$\frac{1}{5}$$\overrightarrow{CM}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com