函数f(x)=x2-4x-4.
(1)求f(x)在闭区间[0,3]上的最大值和最小值.
(2)设f(x)在闭区间[t,t+1](t∈R)上的最小值记为g(t),试写出g(t)的函数关系式.
【答案】
分析:(1)由f(x)=x
2-4x-4=(x-2)
2-8,能求出f(x)在闭区间[0,3]上的最大值和最小值.
(2)当t>2时,f(x)在[t,t+1]上是增函数,由g(t)=f(t)=t
2-4t-4,利用分类讨论思想能求出g(t).
解答:解:(1)f(x)=x
2-4x-4=(x-2)
2-8.
二次函数f(x)的图象是一条开口方向向上的抛物线,对称轴方程是x=2,…(2分)
所以,函数f(x)在[0,2]上单调递减,
f(x)在[2,3]上单调递增.…(4分)
f(0)=-4,f(2)=-8,f(3)=-7.
所以,当x=2时,f(x)
min=-8,当x=0时,f(x)
max=-4.…(6分)
(2)当t>2时,f(x)在[t,t+1]上是增函数.
∴g(t)=f(t)=t
2-4t-4.…(8分)
当t≤2≤t+1,即1≤t≤2时,g(t)=f(2)=-8.…(10分)
当t+1<2,即t<1时,f(x)在区间[t,t+1]上是减函数.
∴g(t)=f(t+1)=t
2-2t-7.…(12分)
综上可知:g(t)=
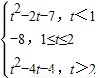
.…(14分)
点评:本题考查函数的最值的求法,考查函数的解析式的求法,解题时要认真审题,注意配方法和分类讨论法的合理运用.

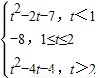 .…(14分)
.…(14分)

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案