
【题目】如图,四棱锥P-ABCD中,底面ABCD为梯形,PD⊥底面ABCD,AB∥CD,AD⊥CD,AD=AB=1,BC=![]() .
.
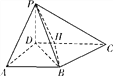
(Ⅰ)求证:平面PBD⊥平面PBC;
(Ⅱ)设H为CD上一点,满足![]() =2
=2![]() ,若直线PC与平面PBD所成的角的正切值为
,若直线PC与平面PBD所成的角的正切值为![]() ,求二面角H-PB-C的余弦值.
,求二面角H-PB-C的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)通过勾股定理可得BC⊥BD,利用面面垂直的判定定理即得结论;
(Ⅱ)通过题意以D为原点,DA、DC、DP分别为x、y、z轴建立坐标系,所求二面角的余弦值即为平面HPB的一个法向量与平面PBC的一个法向量的夹角的余弦值,计算即可.
试题解析:
(Ⅰ)证明:由AD⊥CD,AB∥CD,AD=AB=1BD=![]() ,
,
又BC=![]() ,∴CD=2,∴BC⊥BD,因为PD⊥底面ABCD,∴BC⊥PD.
,∴CD=2,∴BC⊥BD,因为PD⊥底面ABCD,∴BC⊥PD.
因为PD∩BD=D,所以BC⊥平面PBD,所以平面PBD⊥平面PBC.
(Ⅱ)由(Ⅰ)可知∠BPC为PC与底面PBD所成的角.
所以tan∠BPC=![]() ,
,
所以PB=![]() ,PD=1,又
,PD=1,又![]() =2
=2![]() 及CD=2,
及CD=2,
可得CH=![]() ,DH=
,DH=![]() .
.
以D点为坐标原点,DA,DC,DP分别x,y,z轴建立空间坐标系,则B(1,1,0),P(0,0,1),C(0,2,0),H![]() .
.
设平面HPB的法向量为n=(x1,y1,z1),
则由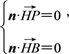 得
得 取n=(1,-3,-2),
取n=(1,-3,-2),
设平面PBC的法向量为m=(x2,y2,z2),
则由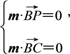 得
得![]() 取m=(1,1,2).
取m=(1,1,2).
所以cos〈m·n〉=![]() =-
=-![]() ,所以二面角H-PB-C余弦值为
,所以二面角H-PB-C余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
男 | 女 | 总计 | |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() ,算得
,算得 ![]()
参照独立性检验附表,得到的正确结论是( )
A.有99%的把握认为“选择过马路的方式与性别有关”
B.有99%的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=cos(ωx+φ)(ω>0,﹣ ![]() <φ<0)的最小正周期为π,且f(
<φ<0)的最小正周期为π,且f( ![]() )=
)= ![]() .
. 
(1)求ω和φ的值;
(2)在给定坐标系中作出函数f(x)在[0,π]上的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 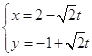 (
( ![]() 为参数),以原点
为参数),以原点 ![]() 为极点,以
为极点,以 ![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)求曲线 ![]() 的普通方程与曲线
的普通方程与曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)试判断曲线 ![]() 与
与 ![]() 是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
是否存在两个交点,若存在,求出两交点间的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合U={x∈N|0<x≤8},S={1,2,4,5},T={3,5,7},则S∩(UT)=( )
A.{1,2,4}
B.{1,2,3,4,5,7}
C.{1,2}
D.{1,2,4,5,6,8}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线![]() (
( ![]() 是参数)和定点
是参数)和定点![]() , F1 , F2 是圆锥曲线的左、右焦点.
, F1 , F2 是圆锥曲线的左、右焦点.
(1)求经过点 F2 且垂直于直线 AF1 的直线 l 的参数方程;
(2)设 P 为曲线 C 上的动点,求 P 到直线 l 距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com