关于x的方程x3+|3x-a|-2=0在(0,2)上有两个不同的解,则实数a的范围为________.
(2,4)
分析:将方程x
3+|3x-a|-2=0恰有两个不同的实根,转化为一个函数y=x
3-2的图象与折线y=-|3x-a|的位置关系研究.
解答:
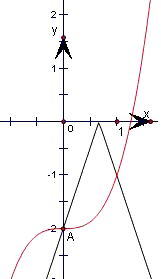
解:方程x
3+|3x-a|-2=0化为:
方程x
3-2=-|3x-a|,
令 y=x
3-2,y=-|3x-a|,
y=-|3x-a|表示过斜率为过点(

,0)的折线直线系,分别画出它们的图象,如图.
①折线中的直线y=3x-a过曲线y=x
3-2与y轴的交点A(0,-2)时有a=2,
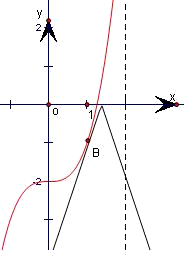
②折线中的直线y=3x-a与曲线y=x
3-2相切时,设切点B(m,n),(m>0).
由于y′=3x
2,则切线的斜率k=3m
2,
且3m
2=3,?m=1,
得切点坐标B(1,-1),代入折线y=3x-a得:a=4,
结合图象得,若关于x的方程x
3+|3x-a|-2=0在(0,2)上有两个不同的解,则实数a的范围为 (2,4)
故答案为:(2,4).
点评:本题主要考查根的存在性及根的个数判断,解答关键是利用直线与曲线的位置关系,要注意导数工具的应用和转化思想的应用.

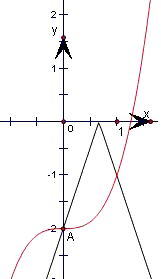
 解:方程x3+|3x-a|-2=0化为:
解:方程x3+|3x-a|-2=0化为: ,0)的折线直线系,分别画出它们的图象,如图.
,0)的折线直线系,分别画出它们的图象,如图.

 字词句段篇系列答案
字词句段篇系列答案