
【题目】如图,在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的左顶点为A(﹣2,0),离心率为
=1(a>b>0)的左顶点为A(﹣2,0),离心率为 ![]() ,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.
,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.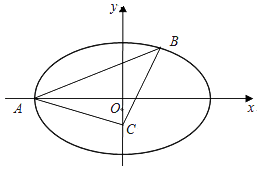
(1)求椭圆E的标准方程;
(2)若△ABC是以点C为直角顶点的等腰直角三角形,求直线l的方程.
【答案】
(1)解:由题意可得:  ,从而有b2=a2﹣c2=3,
,从而有b2=a2﹣c2=3,
所以椭圆E的标准方程为: ![]()
(2)解:设直线l的方程为y=k(x+2),代入为: ![]() ,
,
得(3+4k2)x2+16k2x+16k2﹣12=0
因为x=﹣2为该方程的一个根,解得B( ![]() ,
, ![]() ),
),
设C(x0,y0),由kACkBC=﹣1,得: 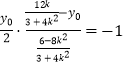 ,
,
即:(3+4k2)y02﹣12ky0+(16k2﹣12)=0 ①
由AC=BC,即AC2=BC2,得4+y02=( ![]() )2+(y0﹣
)2+(y0﹣ ![]() )2,
)2,
即4= ![]() +(
+( ![]() )2﹣
)2﹣ ![]() ,
,
即4(3+4k2)2=(6﹣8k2)2+144k2﹣24(3+4k2)y0…①,
所以k=0或y0= ![]() ,
,
当k=0时,直线l的方程为y=0,
当y0= ![]() 时,代入①得16k4+7k2﹣9=0,解得k=
时,代入①得16k4+7k2﹣9=0,解得k= ![]() ,
,
此时直线l的方程为y=± ![]() (x+2)
(x+2)
综上,直线l的方程为y=0,y=± ![]() (x+2)
(x+2)
【解析】(1)根据椭圆的特性可得a、b的值进而得到椭圆的方程。(2)联立椭圆和直线的方程,点A在椭圆上,解得点B的坐标,利用设而不求法设出点C
的坐标,根据两条直线垂直斜率值即为-1得到关于x0、y0的一个方程,根据AC=BC得到另一个关于x0、y0的方程,联立两式解得k和y0的值,分情况讨论
当k=0时,直线l的方程为y=0,当![]() 时,求出k= ±
时,求出k= ± ![]() ,进而得到直线的方程。
,进而得到直线的方程。


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣x﹣1)ex .
(1)求函数f(x)的单调区间.
(2)若方程a( ![]() +1)+ex=ex在(0,1)内有解,求实数a的取值范围.
+1)+ex=ex在(0,1)内有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知总体的各个体的值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5,平均数为10.若要使该总体的方差最小,则a、b的取值分别是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记函数f(x)=lg(1﹣ax2)的定义域、值域分别为集合A,B.
(1)当a=1时,求A∩B;
(2)若“x∈A”是“x∈B”的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在上学路上要经过A、B、C三个带有红绿灯的路口.已知他在A、B、C三个路口遇到红灯的概率依次是 ![]() 、
、 ![]() 、
、 ![]() ,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
(1)求这名同学在上学路上在第三个路口首次遇到红灯的概率;,
(2)求这名同学在上学路上因遇到红灯停留的总时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数x,y满足的约束条件 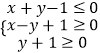 ,将一颗骰子投掷两次得到的点数分别为a,b,则函数z=2ax+by在点(2,﹣1)处取得最大值的概率为( )
,将一颗骰子投掷两次得到的点数分别为a,b,则函数z=2ax+by在点(2,﹣1)处取得最大值的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com