
【题目】某同学在上学路上要经过A、B、C三个带有红绿灯的路口.已知他在A、B、C三个路口遇到红灯的概率依次是 ![]() 、
、 ![]() 、
、 ![]() ,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
(1)求这名同学在上学路上在第三个路口首次遇到红灯的概率;,
(2)求这名同学在上学路上因遇到红灯停留的总时间.
【答案】
(1)解:设这名同学在上学路上到第三个路口时首次遇到红灯为事件A,
因为事件A等于事件“这名同学在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯”,
所以事件A的概率为P(A)=(1﹣ ![]() )(1﹣
)(1﹣ ![]() )×
)× ![]() =
= ![]()
(2)解:记“这名同学在上学路上因遇到红灯停留的总时间”为ξ,
由题意,可得ξ可能取值为0,40,20,80,60,100,120,140(单位:秒);…
∴即ξ的分布列是:
P(ξ=0)=(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )=
)= ![]() ;
;
P(ξ=40)= ![]() ×(1﹣
×(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )=
)= ![]() ;
;
P(ξ=20)=(1﹣ ![]() )×
)× ![]() ×(1﹣
×(1﹣ ![]() )=
)= ![]() ;
;
P(ξ=80)=(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )×
)× ![]() =
= ![]() ;
;
P(ξ=60)= ![]() ×
× ![]() ×(1﹣
×(1﹣ ![]() )=
)= ![]() ;
;
P(ξ=100)=(1﹣ ![]() )×
)× ![]() ×
× ![]() =
= ![]() ;
;
P(ξ=120)= ![]() ×(1﹣
×(1﹣ ![]() )×
)× ![]() =
= ![]() ;
;
P(ξ=140)= ![]() ×
× ![]() ×
× ![]() =
= ![]()
所以Eξ=40× ![]() +20×
+20× ![]() +80×
+80× ![]() +60×
+60× ![]() +100×
+100× ![]() +120×
+120× ![]() +140×
+140× ![]() =
= ![]() .
.
答:这名同学在上学路上因遇到红灯停留的总时间为 ![]()
【解析】(1)根据概率的几何概型可求出事件A的概率。(2)根据已知得到ξ可能取值,再利用几何概型求出各个概率,列表可得。
【考点精析】解答此题的关键在于理解几何概型的相关知识,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等,以及对离散型随机变量及其分布列的理解,了解在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)判断函数f(x)的奇偶性,并说明理由;
(2)证明:f(x)在(﹣1,+∞)上为增函数;
(3)证明:方程f(x)=0没有负数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的左顶点为A(﹣2,0),离心率为
=1(a>b>0)的左顶点为A(﹣2,0),离心率为 ![]() ,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.
,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.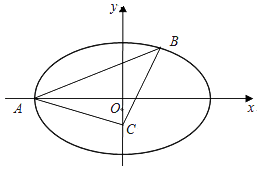
(1)求椭圆E的标准方程;
(2)若△ABC是以点C为直角顶点的等腰直角三角形,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的三个内角分别为A,B,C.向量 ![]() 共线. (Ⅰ)求角C的大小;
共线. (Ⅰ)求角C的大小;
(Ⅱ)设角A,B,C的对边分别是a,b,c,且满足2acosC+c=2b,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a2﹣3a+3)ax是指数函数,
(1)求f(x)的表达式;
(2)判断F(x)=f(x)﹣f(﹣x)的奇偶性,并加以证明
(3)解不等式:loga(1﹣x)>loga(x+2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为函数y=f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)图象的一部分,其中点 ![]() 是图象的一个最高点,点
是图象的一个最高点,点 ![]() 是与点P相邻的图象与x轴的一个交点.
是与点P相邻的图象与x轴的一个交点.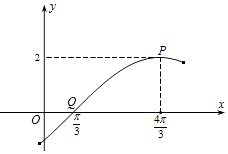
(1)求函数f(x)的解析式;
(2)若将函数f(x)的图象沿x轴向右平移 ![]() 个单位,再把所得图象上每一点的横坐标都变为原来的
个单位,再把所得图象上每一点的横坐标都变为原来的 ![]() (纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的单调递增区间.
(纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如图: 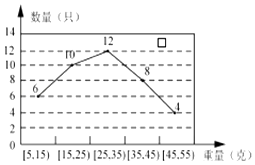
(1)记事件A为:“从这批小龙虾中任取一只,重量不超过35g的小龙虾”,求P(A)的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [5,25) | [25,45) | [45,55] |
按分层抽样抽取10只,再随机抽取3只品尝,记X为抽到二等品的数量,求抽到二级品的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com