
【题目】执行如图所示的流程图,则输出的x值为 . 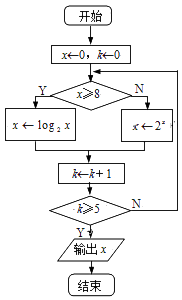
【答案】4
【解析】解:当x=0时,不满足x≥8,故x=1,k=1,不满足退出循环的条件;
当x=1时,不满足x≥8,故x=2,k=2,不满足退出循环的条件;
当x=2时,不满足x≥8,故x=4,k=3,不满足退出循环的条件;
当x=4时,不满足x≥8,故x=16,k=4,不满足退出循环的条件;
当x=16时,满足x≥8,故x=4,k=5,满足退出循环的条件;
故输出的x值为4,
所以答案是:4
【考点精析】根据题目的已知条件,利用程序框图的相关知识可以得到问题的答案,需要掌握程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


科目:高中数学 来源: 题型:
【题目】已知公比为q的等比数列{an}的前6项和S6=21,且4a1 , ![]() ,a2成等差数列.
,a2成等差数列.
(1)求an;
(2)设{bn}是首项为2,公差为﹣a1的等差数列,记{bn}前n项和为Tn , 求Tn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=3x2﹣4ax(a>0)与g(x)=2a2lnx+b有公共点,且在公共点处的切线方程相同,则实数b的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记函数f(x)=lg(1﹣ax2)的定义域、值域分别为集合A,B.
(1)当a=1时,求A∩B;
(2)若“x∈A”是“x∈B”的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SA=SC,AB⊥AC,D为BC的中点,E为AC上一点,且DE∥平面SAB.求证: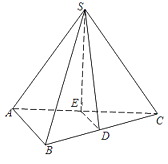
(1)直线AB∥平面SDE;
(2)平面ABC⊥平面SDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在上学路上要经过A、B、C三个带有红绿灯的路口.已知他在A、B、C三个路口遇到红灯的概率依次是 ![]() 、
、 ![]() 、
、 ![]() ,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
(1)求这名同学在上学路上在第三个路口首次遇到红灯的概率;,
(2)求这名同学在上学路上因遇到红灯停留的总时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足2an+1=an+an+2+k(n∈N* , k∈R),且a1=2,a3+a5=﹣4.
(1)若k=0,求数列{an}的前n项和Sn;
(2)若a4=﹣1,求数列{an}的通项公式an .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com