
【题目】如图,在三棱锥S﹣ABC中,SA=SC,AB⊥AC,D为BC的中点,E为AC上一点,且DE∥平面SAB.求证: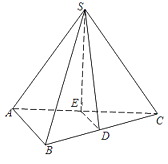
(1)直线AB∥平面SDE;
(2)平面ABC⊥平面SDE.
【答案】
(1)证明:因为DE∥平面SAB,DE平面ABC,平面SAB∩平面ABC=AB,
所以DE∥AB,
因为DE平面SDE,AB平面SDE,
所以AB∥平面SDE
(2)证明:因为D为BC的中点,DE∥AB,
所以E为AC的中点.
又因为SA=SC,所以SE⊥AC,
又AB⊥AC,DE∥AB,
所以DE⊥AC,
∵DE平面SDE,SE平面SDE,DE∩SE=E,
所以AC⊥平面SDE,
因为AC平面ABC,
所以平面ABC⊥平面SDE
【解析】(1)由线面平行的性质定理可得出DE∥AB,再由线面平行的判定定理得到线面平行。(2)由已知可得SE⊥AC,再利用平行的传递性可得DE⊥AC,由线面垂直的判定定理可得AC⊥平面SDE,,进而得到面面垂直。
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者对本队赢得一分,答错得零分.假设甲队中每人答对的概率均为 ![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ![]() ,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.
(Ⅰ)求随机变量ξ的分布列和数学期望;
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中正确是( )
A.函数y=ax(a>0且a≠1)与函数 ![]() (a>0且a≠1)的值域相同
(a>0且a≠1)的值域相同
B.函数y=![]() 与y=
与y=![]() 的值域相同
的值域相同
C.函数 ![]() 与
与 ![]() 都是奇函数
都是奇函数
D.函数y=![]() 与y=2x﹣1在区间[0,+∞)上都是增函数.
与y=2x﹣1在区间[0,+∞)上都是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=2acosθ(a>0),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为 ![]() (t为参数),若直线l与圆C恒有公共点,求实数a的取值范围.
(t为参数),若直线l与圆C恒有公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的三个内角分别为A,B,C.向量 ![]() 共线. (Ⅰ)求角C的大小;
共线. (Ⅰ)求角C的大小;
(Ⅱ)设角A,B,C的对边分别是a,b,c,且满足2acosC+c=2b,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的正整数k,如果各项均为正数的数列{an}满足:对任意正整数n(n>k),an﹣kan﹣k+1…an﹣1an+1…an+k﹣1an+k=an2k总成立,那么称{an}是“Q(k)数列”.
(1)若{an}是各项均为正数的等比数列,判断{an}是否为“Q(2)数列”,并说明理由;
(2)若{an}既是“Q(2)数列”,又是“Q(3)数列”,求证:{an}是等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com