
分析 设t=-x2+2x,利用换元法结合复合函数单调性之间的关系进行求解即可.
解答 解:设t=-x2+2x,则t=-(x-1)2+1,
对称轴为x=1,
则y=($\frac{1}{2}$)t为减函数,
要求函数y=($\frac{1}{2}$)${\;}^{2x-{x}^{2}}$的单调减区间,即求函数t=-x2+2x的单调递增区间,
当-4≤x≤1时,函数t=-x2+2x为增函数,
则函数y=($\frac{1}{2}$)${\;}^{2x-{x}^{2}}$(x∈[-4,7])的单调递减区间是[-4,1],
故答案为:[-4,1]
点评 本题主要考查函数单调区间的求解,利用换元法结合复合函数单调性之间的关系是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
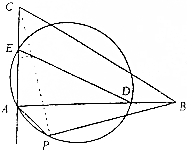 如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第4名学生操作了n台设备 | B. | 第4名学生操作了3台设备 | ||
| C. | 第3名学生操作了n台设备 | D. | 第3名学生操作了4台设备 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
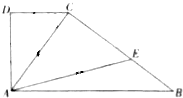 如图所示直角梯形ABCD中,∠BAD=∠ADC=90°,∠ACD=60°,AB=3DC=3,若线段BC上存在点E,使得AC、AE、AB成等比数列,则$\frac{CE}{CB}$等于( )
如图所示直角梯形ABCD中,∠BAD=∠ADC=90°,∠ACD=60°,AB=3DC=3,若线段BC上存在点E,使得AC、AE、AB成等比数列,则$\frac{CE}{CB}$等于( )| A. | $\frac{1+\sqrt{15}}{7}$ | B. | $\frac{6-\sqrt{15}}{7}$ | C. | $\frac{\sqrt{87}-9}{7}$ | D. | $\frac{18-\sqrt{87}}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com